Интегрирование по частям

Пусть даны две произвольные дифференцируемые функции и, тогда

то есть

Проинтегрируем обе части последнего тождества

,

откуда получим формулу интегрирования по частям:

XII. .

Формула интегрирования по частям обычно применяется для вычисления интегралов следующих двух видов:

1)

2) и др.

Здесь Р„(х) — многочлен п-ой степени.

Для интегралов первого вида за и принимают многочлен Р„(х), а за dv —оставшуюся часть подынтегральных выражений или

При разбиения на части интегралов второго вида за и принимают функцию ln^k x, arcsin аx или arcos аx, а за dv — выражение P_n(x)dx.

Замечание: необходимо следить за тем, чтобы все участники исходного подынтегрального выражения вошли в какую-либо часть разбиения.

Пример 1. Найдем

.

Разобьем подынтегральное выражение так, чтобы в дальнейшем избавиться в нем от рационального множителя х. Пусть и = х, dv - e^xdx, тогда du = dx, a v = ʃe^xdx = e^x. Получим

Кроме формулы XII, здесь мы использовали формулу IIIа.

Пример 2. Найдем

.

Будем оформлять разбиение подынтегрального выражения на части в фигурных скобках:

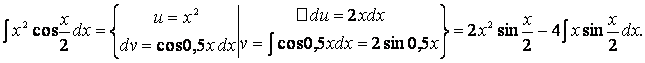
Легко видеть, что полученный после такого разбиения интеграл хотя и проще исходного (степень рациональной функции стала ниже), однако он требует еще одного применения формулы XII:

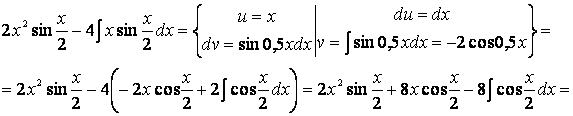
Пример 3. Найдем

.

Этот интеграл относится к интегралам второго вида, поэтому за и при разбиении следует принять функцию ln x: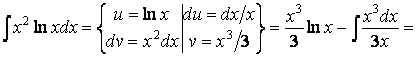

Пример 4. Найдем

.

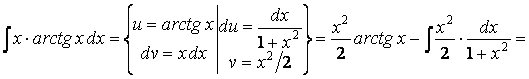
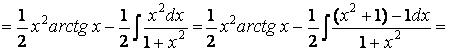
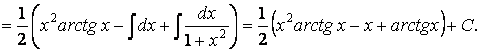
Замечание: область применения метода интегрирования по частям не исчерпывается приведенными выше видами интегралов. При выборе способа разбиения подынтегрального выражения важно, чтобы интеграл, полученный в результате применения формулы ХП, был явно проще исходного.

Пример 5. Найдем

.

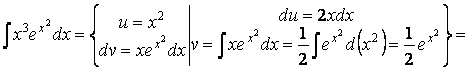
Пример 6. Найдем

.

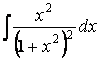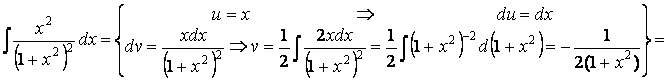
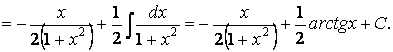
Пример 7. Найдем

.

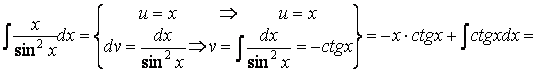
Пример 8. Найдем

.

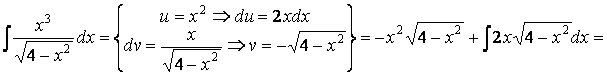
Пример 9. Найдем

.

Выполним сначала подстановку , тогда х = z², a . Полученный относительно z интеграл возьмем по частям.

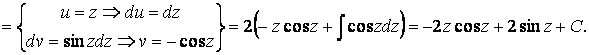
Вернемся к исходной переменной х:

Пример 10. Найдем

.

Умножив и поделив подынтегральное выражение на , получим

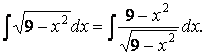
После почленного деления в подынтегральном выражении и использования пятого свойства интегралов имеем

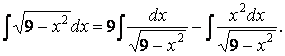
Первый из слагаемых интегралов—табличный (формула X), а ко второму применим формулу интегрирования по частям:

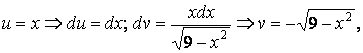
тогда

Здесь через J мы обозначили исходный интеграл . Решая полученное уравнение

,

находим:

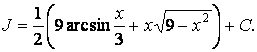
Пример 11.Найдем

.

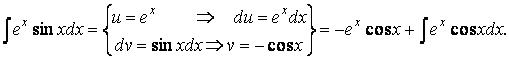
В результате применения формулы XII получен интеграл того же вида, что и исходный. Используем подобное разбиение на части еще раз.

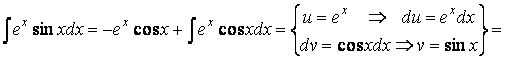
Здесь через J мы вновь обозначили исходный интеграл. Решая далее полученное уравнение относительно J, найдем:

Пример 12. Найдем

.
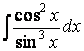
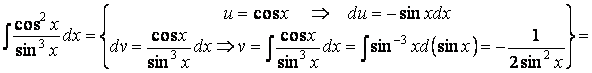