Метод замены переменной

Кроме рассмотренных нами приемов работы с тригонометрическими интегралами, следует отметить еще один. Любой интеграл вида

(здесь R(sinx, cosx) — рациональная функция от sinx и cosx) может быть сведен к интегралу от рациональной функции заменой переменной

,

где

Действительно,

Т.е. при такой замене sinx, cosx,dx выражаются рационально через новую переменную t и интеграл принимает вид , где —некоторая рациональная функция.

Пример 1. Найдем

.

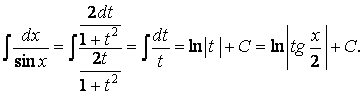
Здесь мы использовали указанную подстановку и табличную формулу II. Для получения окончательного ответа мы вернулись к старой переменной х, используя формулу t = tgх.

Подстановка, использованная в рассмотренном примере, называется универсальной тригонометрической подстановкой.

В общем случае метод подстановки, или метод замены переменной, описывается формулами

, где

, где .

Здесь вторая формула получается из первой перестановкой переменных х и t, а также ее правой и левой части.

Пример 2. Найдем

.

Выполним подстановку , тогда

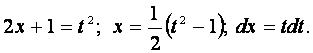
Получим

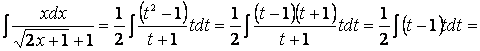
Пример 3. Найдем

.

Выполним подстановку , тогда , a .Тогда

Под интегралом стоит неправильная дробь. Выделив целую часть, получим

Здесь были использованы формулы I и II. Вернемся теперь к старой переменной:

Пример 4. Найдем

.

Положим, , тогда , а корень

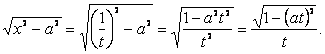
Выполнив подстановку в исходный интеграл, получим

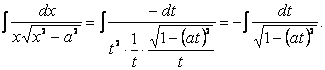
Для использования формулы X таблицы интегралов необходимо создать дифференциал выражения at: d(at)=a ^.dt. Для этого умножим и поделим подынтегральное выражение на число а, вынесем за знак интеграла ненужный нам коэффициент и получим

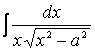
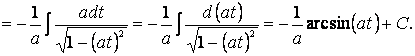
Возвращаясь к старой переменной по формуле , окончательно найдем

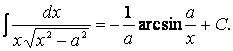
Пример 5. Найдем

.

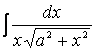Используем подстановку: х = а tg t. Тогда

откуда

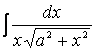
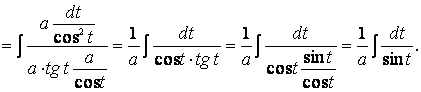
Такой интеграл нами был взят в примере 1. Воспользуемся полученным результатом и вернемся к исходной переменной, используя обратную подстановку:

,

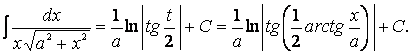
Пример 6. Найдем

,

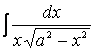воспользовавшись подстановкой Тогда

Получим

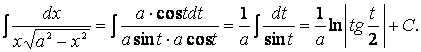
Или, вернувшись к старой переменной, получим

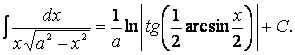
Пример 7. Найдем

.

Воспользуемся подстановкой

Тогда

где

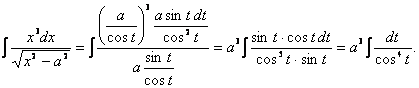
Представим подынтегральную функцию в виде

получим

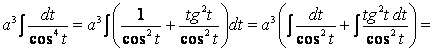
Возвращаясь к старой переменной, будем иметь

Обобщим опыт, приобретенный при решении последних четырех примеров.

Интеграл вида

,

где п — целое число, берется после одной из использованных выше подстановок:

1) 2) 3) 4) или

Причем первая подстановка используется, если натуральная степень переменной стоит перед корнем в знаменателе, вторая—когда корень в подынтегральной функции имеет вид:

Если же корень имеет вид , то эффективна третья подстановка:

Четвертая используется обычно, когда корень имеет вид

Как видим, при рассмотренных тригонометрических подстановках подынтегральная функция становится рациональной относительно функций sinх и cosх.