Основные понятия ФНП
Пусть ![]() некоторое множество
точек
некоторое множество
точек ![]()
![]() -мерного пространства с координатами
-мерного пространства с координатами ![]() . Если каждой точке
. Если каждой точке ![]() поставлено в
соответствие единственное действительное число
поставлено в
соответствие единственное действительное число ![]() , то говорят, что на множестве
, то говорят, что на множестве ![]() задана функция
задана функция ![]() переменных
переменных ![]() .
.
При этом множество ![]() называется областью
определения функции
называется областью
определения функции ![]() .
.
Например, площадь
поверхности прямоугольного параллелепипеда с размерами ![]() ,
, ![]() ,
, ![]()
![]() является функцией трех
переменных
является функцией трех
переменных ![]() ,
, ![]() ,
, ![]() , определенной в первом октанте, т.е. на множестве
, определенной в первом октанте, т.е. на множестве
![]() :
: 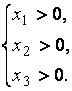
Объем конуса с радиусом
основания ![]() и высотой
и высотой ![]()
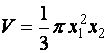 является функцией двух
переменных
является функцией двух
переменных ![]() ,
, ![]() , определенной в первом квадранте, т.е. на множестве
, определенной в первом квадранте, т.е. на множестве ![]() :
: 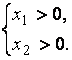
Заметим, что для функции
двух переменных аргументы удобнее обозначать буквами ![]() и
и ![]() (вместо
(вместо ![]() и
и ![]() ), а для функции трех переменных - буквами
), а для функции трех переменных - буквами ![]() ,
,![]() и
и ![]() ( вместо
( вместо ![]() ,
, ![]() и
и ![]() ).
).
Если у функции двух
переменных ![]() зафиксировать одну из
переменных, например положить
зафиксировать одну из
переменных, например положить ![]() , то мы получим некоторую функцию одной переменной
, то мы получим некоторую функцию одной переменной ![]() :
: ![]() .
.
Если при этом функция ![]() имеет производную в
точке
имеет производную в
точке ![]() , то ее значение
, то ее значение ![]() называется частной производной по
называется частной производной по ![]() функции
функции ![]() в точке
в точке ![]() и обозначается
и обозначается 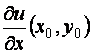 или
или ![]() .
.
Зафиксировав переменную ![]() , аналогично придем к понятию частной производной по
, аналогично придем к понятию частной производной по ![]() от функции двух
переменных
от функции двух
переменных ![]() .
.
Для функции любого числа переменных
естественно ввести частные производные по какому-либо из аргументов путем
предварительного фиксирования всех остальных аргументов.
Пример 1. Найдите частные производные функции ![]() .
.
Решение.
![]() ,
, 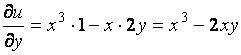 .
.
Пример 2. Найдите частные производные функции ![]() .
.
Решение.
![]() ,
,
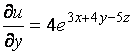 ,
,
![]() .
.
Обобщением понятия частной производной
по какому-либо из аргументов ФНП является понятие производной по направлению.
Если направление ![]() на плоскости (в
трехмерном пространстве) образует с осями координат углы
на плоскости (в
трехмерном пространстве) образует с осями координат углы ![]() и
и ![]()
![]() (
(![]() ,
,![]() и
и ![]() ), то производной функции
), то производной функции ![]()
![]() в точке
в точке ![]()
![]() по направлению
по направлению ![]() называется выражение
называется выражение
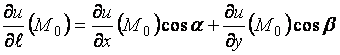
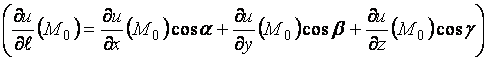 .
.
Пример 3. Найдите производную функции ![]() в точке
в точке ![]() по направлению вектора
по направлению вектора
![]() .
.
Решение.
Вычисляем
частные производные функции ![]() в произвольной точке
в произвольной точке
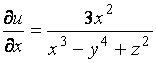 ,
,  ,
, 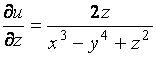 ,
,
а затем в точке ![]() :
:
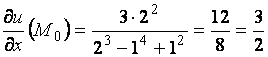 ,
, 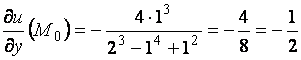 ,
,
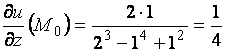 .
.
Находим направляющие косинусы
вектора ![]() :
:
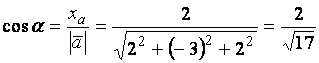 ,
,
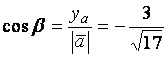 ,
, 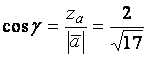 .
.
Тогда
 .
.
Легко заметить, что частные
производные являются производными по направлению соответствующей оси координат:
![]() есть производная
функции
есть производная
функции ![]() по направлению оси
по направлению оси ![]() ,
, ![]() есть производная
функции
есть производная
функции ![]() по направлению оси
по направлению оси ![]() ,
, ![]() есть производная
функции
есть производная
функции ![]() по направлению оси
по направлению оси ![]() .
.
Обратим внимание на то
обстоятельство, что выражение для производной по направлению можно
рассматривать как скалярное произведение двух векторов: вектора ![]() - единичного вектора заданного направления
- единичного вектора заданного направления
![]() и некоторого вектора
и некоторого вектора
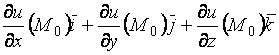 .
.
Вектор с координатами ![]() ,
, ![]() ,
, ![]() принято называть вектором градиента функции
принято называть вектором градиента функции ![]() или просто градиентом этой функции и обозначать
или просто градиентом этой функции и обозначать 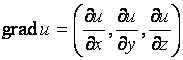 .
.
Пример 4. Найдите градиент функции  в произвольной точке.
в произвольной точке.
Решение.
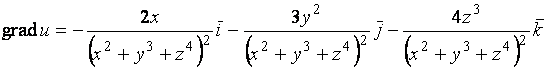 .
.
С понятием частной производной
легко по аналогии с производной и дифференциалом функции одной переменной
связать понятие частного дифференциала:
![]() ,
, 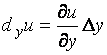 ,
, ![]() .
.
Здесь ![]() ,
, ![]() ,
, ![]() - частные
дифференциалы функции
- частные
дифференциалы функции ![]() по переменной
по переменной ![]() ,
,![]() и
и ![]() , соответственно, а
, соответственно, а ![]() ,
, ![]() ,
, ![]() - приращения этих независимых переменных.
Однако для ФНП можно ввести еще одно понятие - полного дифференциала - суммы частных
дифференциалов по всем независимым переменным:
- приращения этих независимых переменных.
Однако для ФНП можно ввести еще одно понятие - полного дифференциала - суммы частных
дифференциалов по всем независимым переменным:
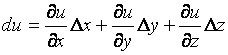 или
или 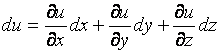 .
.
Пример 5. Найдите полный дифференциал функции ![]() в произвольной
(допустимой) точке.
в произвольной
(допустимой) точке.
Решение.
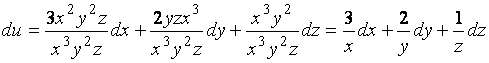 .
.
Полный дифференциал ФНП по
аналогии с функцией одной переменной может применяться для приближенного вычисления
значений функций нескольких переменных с помощью приближенной формулы ![]() , где
, где ![]() - приращение функции при переходе из точки
- приращение функции при переходе из точки ![]() к точке
к точке ![]() ,
, ![]() - полный дифференциал функции
- полный дифференциал функции ![]() в точке
в точке ![]() , соответствующий приращениям
, соответствующий приращениям ![]() ,
, ![]() ,
, ![]() ее аргументов.
ее аргументов.
Формула для
вычисления значений функции трех переменных имеет вид
![]()
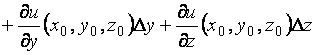 .
.
Пример 6. Вычислите приближенно с помощью дифференциала ![]() .
.
Решение.
Введем функцию ![]() и возьмем
и возьмем ![]() ,
, ![]() ,
, ![]() , тогда
, тогда
![]() ,
, ![]() ,
, ![]() .
.
 ,
,  ,
,
 .
.
В точке ![]()
![]() ,
,
![]() ,
, 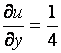 ,
, ![]() .
.
Тогда
![]()
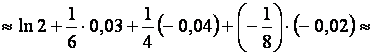
![]() .
.