Общая схема исследования функций
и построения их графиков
При исследовании функций и
построении их графиков целесообразно пользоваться следующей схемой.
1. Нахождение области
определения функции.
2. Исследование функции на
четность и нечетность.
3. Установление области
непрерывности функции и точек разрыва.
Отыскание вертикальных асимптот.
4. Исследование поведения
функции при 
(если она там
определена). Отыскание горизонтальных и наклонных асимптот.
5. Нахождение экстремумов и
интервалов монотонности функции. Составление таблицы.
6. Нахождение интервалов
выпуклости и вогнутости и точек перегиба графика функции.
7. Нахождение точек пересечения
графика функции с осями, интервалов знакопостоянства функции. Составление таблицы. Отыскание
дополнительных точек для построения графика.
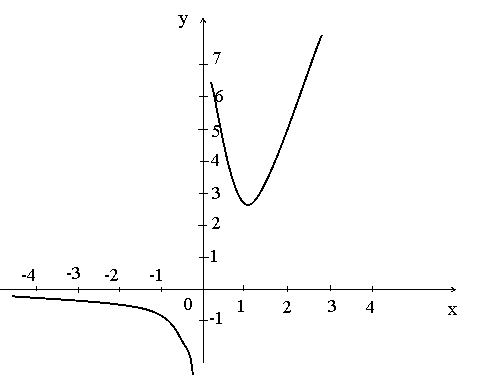
8. Построение графика функции.
Пример.
Исследуйте функцию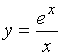 
и постройте ее график.
Решение.
1. Область определения функции 
.
2. 
, 
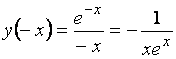и 
. Следовательно, данная функция ни четная, ни нечетная.
3. Функция непрерывна в области
определения, как частное двух непрерывных функций. Исследуем точку 
:
, 
.
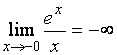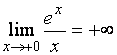Поэтому - точка разрыва функции с бесконечным скачком,
а прямая - вертикальная асимптота графика функции.
4. Вычислим пределы 
при .
Так как 
, то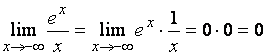 
. Следовательно, прямая 
- левосторонняя горизонтальная асимптота
графика.
С другой стороны,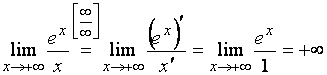 
.
Правосторонней
горизонтальной асимптоты не существует.
Будем искать правостороннюю
наклонную асимптоту.
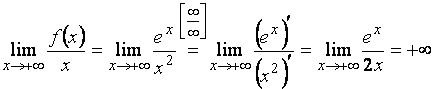, так как уже был вычислен
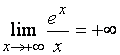. При 
нет асимптоты ни горизонтальной, ни наклонной.
5. Находим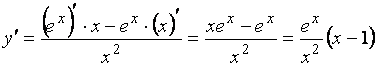 
.
Производная равна нулю в точке
.
Составляем
таблицу.
|
|
|
|
|
|
|
|
- |
- |
|
+ |
|
|
убывает |
убывает |
|
возрастает |
|
|
|
|
|
|
.
6. Найдем вторую производную.
.
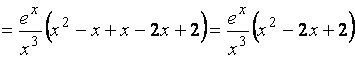не обращается в нуль
ни в одной точке, так как 
, 
при всех 
. Но не существует в точке .
|
Составляем таблицу. |
|
|
|
|
|
|
- |
+ |
|
|
Гра- фик |
выпуклый |
вогнутый |
7. Точка не входит в область
определения. Поэтому график не пересекает ось 
.
Уравнение не имеет решений, так
как при всех . Следовательно, ось 
график тоже не
пересекает. Функция отрицательна при 
и положительна при 
. Найдем несколько дополнительных точек для построения
графика.
|
|
-3 |
-2 |
-1 |
2 |
3 |
0,5 |
-0,5 |
|
|
-0,02 |
-0,07 |
-0,37 |
3,69 |
6,66 |
-1,21 |
3,30 |
|
|
|
,
,
,
,
,
,
.
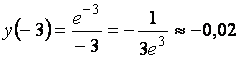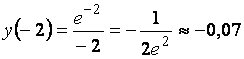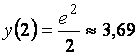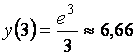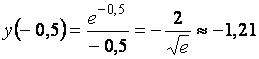