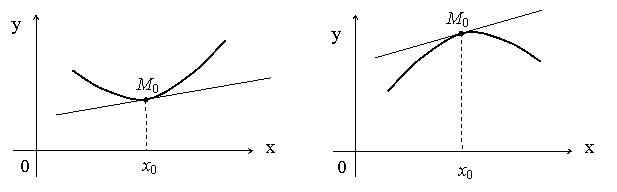Отыскание интервалов
выпуклости и вогнутости
и точек перегиба графика функции
Определение. Говорят,
что график функции ![]() является выпуклым
(вогнутым) в точке
является выпуклым
(вогнутым) в точке ![]()
![]() (в точке
(в точке ![]() ), если в некоторой
окрестности точки
), если в некоторой
окрестности точки ![]() он лежит ниже (выше)
касательной, проведенной к графику в точке
он лежит ниже (выше)
касательной, проведенной к графику в точке ![]() .
.
|
|
|
|
|
В точке |
В точке |
|
Определение. Говорят,
что график функции является выпуклым (вогнутым) в некотором промежутке ![]() , если он выпуклый (вогнутый) в каждой точке этого промежутка.
, если он выпуклый (вогнутый) в каждой точке этого промежутка.
Достаточное условие выпуклости или вогнутости графика функции дает следующая теорема. Если вторая производная функции отрицательна (положительна) в некотором интервале, то график функции - выпуклый (вогнутый) в этом интервале.
Пусть функция ![]() непрерывна в некоторой
окрестности точки
непрерывна в некоторой
окрестности точки ![]() и ее график имеет в
этой точке касательную хотя бы вертикальную (что соответствует наличию
производной у функции
и ее график имеет в
этой точке касательную хотя бы вертикальную (что соответствует наличию
производной у функции ![]() в точке
в точке ![]() , хотя бы бесконечной).
, хотя бы бесконечной).
Если в этом случае точка ![]() отделяет выпуклую
часть графика от вогнутой, то она называется точкой перегиба графика функции.
отделяет выпуклую
часть графика от вогнутой, то она называется точкой перегиба графика функции.
Необходимое
условие существования точки перегиба
Теорема. Если
существует вторая производная ![]() в точке перегиба
в точке перегиба ![]() графика функции, то
она в этой точке равна нулю, т.е.
графика функции, то
она в этой точке равна нулю, т.е. ![]() .
.
Достаточное
условие существования точки перегиба
Теорема. Если вторая
производная ![]() при переходе через
точку
при переходе через
точку ![]() меняет знак, а график
функции имеет в точке
меняет знак, а график
функции имеет в точке ![]() касательную, хотя бы
вертикальную, то точка
касательную, хотя бы
вертикальную, то точка ![]() является точкой
перегиба графика функции
является точкой
перегиба графика функции ![]() .
.
Отсюда вытекает следующий порядок
исследования графика функции на выпуклость, вогнутость и точки перегиба.
1. Находим область определения
функции, если она не задана.
2. Находим вторую производную
функции.
3. Находим критические точки
первой производной функции, т.е. точки из области определения, в которых вторая
производная равна нулю или не существует.
4. Выясняем знак второй
производной слева и справа от найденных точек и делаем вывод об интервалах выпуклости
и вогнутости и наличии точек перегиба.
5. Находим значения функции в
точках перегиба.
Заметим, что результаты
вычислений удобно оформить в виде таблицы.
Пример.
Найдите точки перегиба и интервалы выпуклости и вогнутости графика функции  .
.
Решение.
1. Область определения функции ![]() .
.
2. 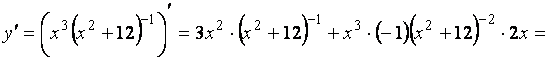
![]() ,
,
![]()
![]()
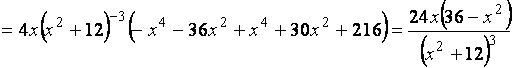 .
.
3. ![]() в точках
в точках ![]() ,
, ![]() ,
, ![]() .
.
4. Составим таблицу.
|
|
|
|
|
|
|
|
|
|
|
+ |
|
- |
|
+ |
|
- |
|
|
|
Точка перегиба |
|
Точка перегиба |
|
Точка перегиба |
|
|
|
|
|
|
|
|
|
|
5. Вычисляем ![]() ,
, ![]() ,
, ![]() .
.
Ответ:
в интервалах ![]() и
и ![]() график выпуклый, в интервалах
график выпуклый, в интервалах
![]() и
и ![]() - вогнутый. Точки
перегиба
- вогнутый. Точки
перегиба 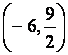 ,
, ![]() ,
, 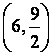 .
.