Отыскание интервалов монотонности функций
Функцию 
мы называем
возрастающей (убывающей) в некотором промежутке 
, если для любых 
и 
из таких, что 
, выполняется неравенство 
.
Теорема (достаточное условие монотонности функции). Если производная 
функции положительна
(отрицательна) в некотором интервале 
, то функция возрастает (убывает) в этом интервале.
Доказательство.
Возьмем два значения
аргумента из интервала и , причем , и применим к отрезку 
теорему Лагранжа:
,
где 
- некоторая точка из интервала 
.
Так как 
по выбору точек, то
знак разности 
совпадает со знаком 
, т.е. со знаком производной в интервале , откуда и следует утверждение теоремы.
Пример.
Найдите интервалы монотонности функции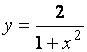 
.
Решение.
. Находим производную функции
.
При 
, т.е. функция возрастает в интервале 
, а если 
, то 
, т.е. функция убывает в интервале 
.
Ответ:
функция возрастает в и убывает в .