Таблица производных

Вычисление пределов функций

с помощью правила Лопиталя

Французскому математику Лопиталю принадлежит следующая теорема.

Пусть функции и одновременно бесконечно малые или бесконечно большие при (). Тогда, если существует (конечный или бесконечный) предел отношения их производных, то существует и предел отношения самих функций и он равен первому пределу, т.е.

.

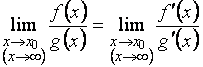Эта теорема, практическое применение которой принято называть правилом Лопиталя, дает возможность раскрывать неопределенности вида и .

Заметим, что отношение бесконечно больших можно представить в виде отношения двух бесконечно малых, и наоборот.

Если и - бесконечно большие, то

,

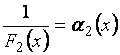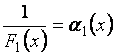где и - бесконечно малые.

Если же и - бесконечно малые, то

,

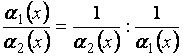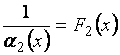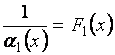где и - бесконечно большие.

К неопределенностям вида и также можно применить правило Лопиталя, предварительно преобразовав их к виду или .

Пример 1. Найдите предел

.

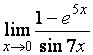Решение.

Имеем неопределенность вида , так как под знаком предела стоит отношение двух бесконечно малых функций. Применяем правило Лопиталя.

.

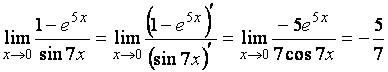Ответ: .

Пример 2. Найдите предел

.

Решение.

Под знаком предела стоит отношение двух бесконечно малых, т.е. имеет место неопределенность вида . Применяем правило Лопиталя.

.

Неопределенность вида сохранилась. Применяем правило Лопиталя еще раз:

.

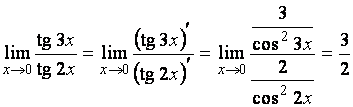Итак,

.

Ответ: .

Пример 3. Найдите предел

.

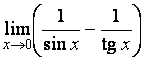Решение.

Под знаком предела стоит разность двух бесконечно больших одного знака, т.е. имеет место неопределенность вида . Преобразуем ее к виду и применим правило Лопиталя.

.

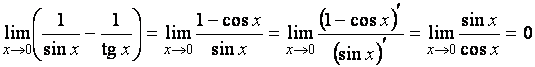Ответ: .