Применение дифференциала
к приближенным вычислениям
Мы установили, что дифференциал функции является частью ее
приращения и отличается от нее на величину 
. Эта величина при 
является бесконечно малой функцией более высокого
порядка, чем 
(при 
), так как
.
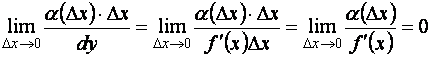Поэтому при достаточно малых
имеет место
приближенное равенство 
или 
, откуда
. (1)
При этом чем меньше , тем точнее значение функции.
Равенство (1) представляет
собой "рабочую формулу" применения дифференциала к приближенным
вычислениям.
Пример. Вычислите приближенно с двумя десятичными знаками 
.
Решение.
Введем функцию 
и в качестве 
возьмем число, наиболее близкое к 
, но такое, чтобы 
легко вычислялся и 
было бы достаточно
малым.
В нашем случае удобно взять 
, тогда 
. Найдем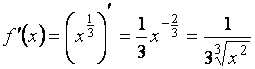 
.
Вычислим 
, 
.
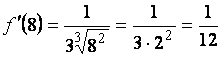Тогда по формуле (1)
.
Ответ:
.