Геометрический смысл дифференциала

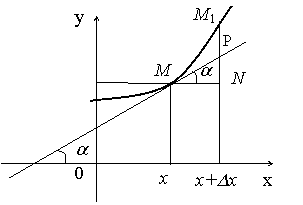На графике функции возьмем произвольную точку и дадим аргументу приращение . При этом функция получит приращение (на рисунке отрезок ).

Проведем касательную к кривой в точке и обозначим угол ее наклона к оси через , тогда . Из треугольника находим , т.е. .

Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции в данной точке, когда аргумент получает приращение .