Логарифмическое дифференцирование
Рассмотрим прием нахождения производных от функций, упрощающихся при логарифмировании, так называемое логарифмическое дифференцирование.
Пример 1. Найдите производную функции 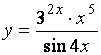 .
.
Решение.
Найдем
![]() .
.
Найдем производные по ![]() от обеих частей
равенства, помня, что
от обеих частей
равенства, помня, что ![]() есть функция от
есть функция от ![]() :
:
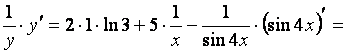
![]()
![]() .
.
В процессе нахождения производных использовалась формула производной сложной функции.
Из полученного равенства находим ![]() :
:
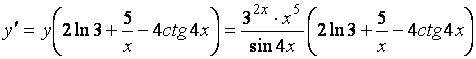 .
.
Пример 2. Найдите производную функции ![]() .
.
Решение.
Дана показательно-степенная функция (у нее переменное основание и переменный показатель). Применим логарифмическое дифференцирование:
![]() ,
,
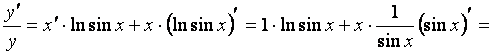
![]() ,
,
откуда
![]() .
.
Замечание. Производная сложной логарифмической функции 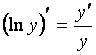 называется логарифмической производной
функции
называется логарифмической производной
функции ![]() .
.
Логарифмическую производную принято называть также относительной
скоростью изменения функции, или темпом изменения функции.