Примеры нахождения производных

некоторых функций ПО ОПРЕДЕЛЕНИЮ

Заметим, что из определения производной может быть получена следующая схема ее отыскания:

1) даем аргументу приращение ;

2) вычисляем приращение функции ;

3) составляем отношение ;

4) находим предел этого отношения при , т.е. (если он существует).

Пример 1. Найдите производную функции .

Решение.

Вычисляем

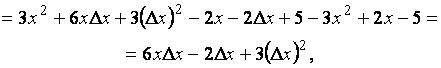
составляем отношение

.

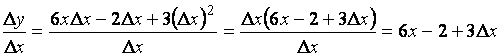Находим предел

.

Итак, , т.е. .

Пример 2. Найдите производную функции , .

Решение.

По определению .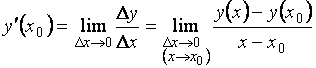

Но

.

Тогда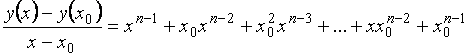

и

.

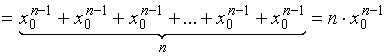Заменяя фиксированную точку на произвольную , получим

.

Пример 3. Найдите производную функции .

Решение.

Вычислим и преобразуем

.

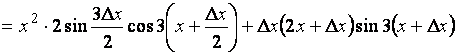Составим отношение и перейдем в нем к пределу при :

.

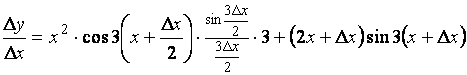По первому замечательному пределу

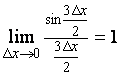и тогда

.

Итак, .

Из рассмотренных примеров видно, что вычисление производных по определению - процесс достаточно громоздкий.

Гораздо удобнее при дифференцировании функций использовать таблицу производных основных элементарных функций и правила дифференцирования.