Задача о скорости

Пусть зависимость пути от времени в данном прямолинейном движении материальной точки выражается уравнением . Дадим согласующееся с нашими наглядными представлениями определение скорости движения (как "быстроты изменения" величины пути с изменением времени).

Пусть - некоторый момент времени. Рассмотрим другой момент времени . Обозначим приращение времени и вычислим соответствующее приращение пути : .

Если отношение остается одним и тем же для различных (равномерное движение), то его и называют скоростью движения.

Если же отношение , как, вообще говоря, и бывает, меняется с изменением , то о нем не имеет смысла говорить как о "скорости движения" вообще; о можно говорить в этом случае лишь как о средней скорости движения за время , протекшее от исходного момента .

Предположим, что уже каким-то образом введено понятие скорости движения в данный момент времени, так что в каждый момент времени эта скорость характеризуется некоторым числом .

Тогда естественно ожидать, что при достаточно малых средняя скорость будет как угодно мало отличаться от (чем меньше промежуток времени , тем меньше скорость успеет измениться за это время и тем ближе средняя скорость к "истинной скорости" в момент ).

Теперь естественно дать такое определение: скоростью прямолинейного движения, с законом , в данный момент времени называется предел средней скорости 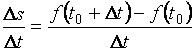(если он существует), когда промежуток времени стремится к нулю, т.е. по определению

(1)

.

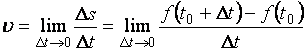Таким образом, чтобы уметь находить скорость прямолинейного движения в данный момент времени , мы должны научиться вычислять предел вида (1).