Теорема (достаточное условие экстремума функции). Пусть функция z=f(x,y) определена в некоторой окрестности критической точки (x₀, y₀), в которой частные производные равны нулю:

,               ;

в этой точке функция имеет непрерывные частные производные второго порядка

, , .

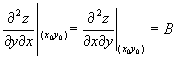Тогда если D=AC-B²>0, то в точке (x₀, y₀) функция имеет экстремум, причем если А<0 - максимум, если А>0 - минимум. В случае D=AC-B²<0 функция экстремума не имеет. Если D=AC-B =0 , то вопрос о наличии экстремума остается открытым.