Простые динамические модели принятия решений о выгодности инвестиций при одной целевой функции

Инвестиционные объекты при использовании динамических моделей связаны с многократными поступлениями и выплатами во времени. Эти поступления и выплаты имеют определенные значения и их можно спрогнозировать и соотнести с конкретными сроками. Исследование динамики показателей поступлений и выплат по нескольким периодам — существенная специфика отличия динамических моделей от статических моделей. Рассмотрим их подробнее с классификацией моделей.

Некоторые финансово-математические преобразования. В динамических моделях платежи производятся в различные сроки, Причем из-за зависимости размера платежей от срока их реализации их нельзя предварительно суммировать, а необходимо проводить финансово-математические преобразования, например, ревальвацию или дисконтирование. Рассмотрим их более подробно.

При ревальвации, или премии {дисконтировании, или вычете), определяют, какую стоимость С приобретет инвестированная к определенному моменту времени сумма капитала (здесь момент времени t= 0) в более поздний срок времени (t=t_n) с учетом начисления процентов и сложных процентов. Если процентная ставка i для всех периодов (исчисление времени в годах) постоянна, то показатель С определяется так:

для ревальвации

(1)

для дисконтирования

(2)

где N — инвестируемый капитал, -коэффициент ревальвации, -коэффициент дисконтирования (для сокращения записи часто принимается, тогда получаем ).

При неодинаковых процентных ставках () для всех периодов наблюдений () имеем, что стоимость инвестированного капитала С определяется так:

(3)

Для подсчета фактической стоимости, т.е. вычисления стоимости в начальный момент времени (t= 0) для ряда платежей одинаковoro размера N, которые ежемесячно осуществляются в конце каждого года в течение t лет, применяется следующая формула:

(4)

здесь называется коэффициентом фактической стоимости периодических поступлений, где k = 1/K— коэффициент восстановления.

Подобным образом можно произвести расчет периодических поступлений путем преобразования имеющейся на нулевой момент времени стоимости N в ряд отнесенных на конец года платежей W равной величины, которые осуществляются до момента t:

(5)

Пример 1. Пусть первоначальный объем инвестируемого капитала составляет 10 тыс. руб. Определить его стоимость через три года, если происходит ревальвация (дисконтирование) и ежегодные процентные ставки составляют: а) постоянную величину, равную = 10%; б) величины, изменяющиеся по годам и соответственно равные ₁ = 10%, ₂=12%, ₃ =15%. Определить фактическую стоимость капитала по ставке 10% и размер периодических поступлений W.

Решение. Подставив численные значения в приведенные выше формулы, получим величину инвестированного капитала при ревальвации через три года:

а) при постоянной ежегодной процентной ставке

С= 10 000 • (1 + 0,10)³ = 13 300 руб.;

б) при изменяющихся процентных ставках

С= 10 000 • (1 + 0,1)(1 +0,12)(1 + 0,15) = 14 168 руб.

Аналогичные показатели при дисконтировании составляют:

а) при постоянной ежегодной процентной ставке

С= 10000 • (1 +0,10)^-3=75l3,15pyб.;

б) при изменяющихся процентных ставках

С = 10 000 • (1 + 0,1)^-1(1 +0,12)^-1(1 + 0,15)^-1= 7 058,16 руб.

Фактическая стоимость инвестиций при ежегодной процентной ставке в 10%, ежегодных платежах в размере 10 тыс. руб. составит:

=10000×[(1+0,1)³-1]/(1+0,1)³×0,1=24868.85 руб.

Размер периодических поступлений составляет:

=10000•(1+0,1)³×0,1/[(1 +0,1)³-1]=4021,15 руб.

Динамические модели оценки выгодности инвестиций.

Этот класс динамических моделей можно подразделить на две основные группы: в моделях первой группы предполагается существование рынка совершенного капитала, когда платежи ревальвируются или дисконтируются по единой ставке процента; в моделях второй группы процентные ставки различаются при вложении и привлечении финансовых средств, что применимо в деятельности банков.

Рассмотрим перечисленные модели более подробно с возможным пояснением на конкретных примерах.

1. Метод определения стоимости капитала предполагает наличие совершенного рынка и служит для оценки альтернатив инвестиций относительно целевой функции стоимости капитала, представляющей собой сумму всех дисконтируемых или ревальвируемых по единой процентной ставке на какой-либо момент времени поступлений и выплат, возникших при инвестировании объекта. Таким образом, по сути стоимость капитала представляет собой фактическую стоимость, характеризующую прирост имущества в денежной форме, приносимый инвестиционным объектом в начале планового периода с учетом процентов. При этом можно использовать следующее правило: инвестиционный объект абсолютно (относительно) выгоден, если стоимость его капитала выше нуля (выше подобного показателя любого иного, предлагаемого на выбор объекта).

Так как расчетная процентная ставка одинакова для всех периодов, то стоимость капитала (СК) на начало планового периода (t=0) определяется так:

(6)

где t - индекс времени; Т- последний момент времени, в который осуществляются платежи; -поступления (выплаты) в момент времени t; -коэффициент дисконтирования на момент времени t.

Рассчитанная для отдельных моментов времени разница () называется чистым платежом (может представлять превышение либо поступлений над выплатами, либо выплат над поступлениями).

Если имеются следующие допущения: а) можно пренебречь налогами и трансфертными платежами; б) с помощью объекта инвестирования выпускают лишь один вид продукции, причем объем производства совпадает с объемом сбыта; в) платежи производятся в следующие сроки: выплаты на приобретение - в начале первого периода (t = 0), текущие поступления и выплаты -по окончании каждого периода, выручка от ликвидации - по окончании срока эксплуатации (t= T), то определить стоимость капитала можно по формуле:

(7)

где t- индекс времени; Т—окончание срока эксплуатации; А₀ -выплаты на приобретение; р_t- цена продажи в момент времени t, a_vt - выплаты за единицу в момент времени t, определяемые объемами сбыта или производства; х_t -объем сбыта или производства в момент времени t; A_ft -выплаты в момент времени t, не зависящие от объемов сбыта или производства; L -выручка от ликвидации; - коэффициент дисконтирования на момент времени t.

Относительную выгодность двух инвестиционных объектов А и В можно определить как разницу стоимостей их капиталов, т.е.

(3.40.)

Если DСК > 0, то объект А является относительно более выгодным по сравнению с объектом В, в противном случае - наоборот (при определении разницы можно пренебречь величинами, одинаково влияющими на оба объекта инвестирования, что упрощает расчет).

Абсолютную выгодность нельзя оценить с помощью инвестиций для определения разницы, а при большом числе альтернатив следует сформировать и оценить множество инвестиций такого рода.

Пример 2. Для расширения производства на предприятии можно применить два инвестиционных проекта А и В, имеющих данные, приведенные в таблице.

Основные сравнительные показатели двух инвестиционных объектов

Основные показатели денежных потоков	Объекты инвестиций
	А	В
Выплаты на приобретение, тыс. руб.	100,0	60, 0
Срок эксплуатации, лет	5	4
Выручка от ликвидации, тыс, руб.	5,0	0
Приток денежных средств, тыс. руб.:
в период t = 1	28,0	22,0
t=2	30,0	26.0
t= 3	35,0	28,0
t= 4	32,0	28,0
t = 5	30,0	-
Расчетная процентная ставка, %	8	8

Требуется оценить абсолютную и относительную выгодность инвестиционных проектов с помощью метода стоимости капитала.

Решение. Определим стоимость капитала инвестиционных объектов А и В согласно вышеприведенной формуле:

=-100000 + 28000 × 1,08^-1 + 30000 ×1,08^-2 +35000× ×1,08^-3+32000×1,08^-4+5000×1,08^-5=26711,59 руб.

Аналогичным образом

СК_B = - 60000 + 22000 • 1,08^-1+26000 • 1,08^-2 + +28000 • 1.08^-3 + +28000 • 1,08^-4 = 1 302,27 руб.

Так как СК_A > 0 и СК_B > 0, то можно сделать вывод об абсолютной выгодности инвестиционных объектов А и В; полученная стоимость капитала в 26 771,59 руб. (1 302,57 руб.) — это прирост имущества в денежной форме, приносимый в результате инвестирования объекта А (объекта В) при t = 0 с учетом выплаты по расчетной процентной ставке 8%, не зависящий от типа финансирования и осуществляемый за счет собственных или заемных средств. Однако объект А имеет более высокую стоимость капитала по сравнению с объектом В и поэтому он вроде бы относительно более выгоден.

Пусть финансирование производится полностью за счет заемных средств в сумме 126 771,59 руб., включающих кредит, взятый на приобретение, равный 100 тыс. руб., и потребительский кредит в размере 26771,59 руб. В конце каждого отчетного периода должна производиться уплата процентов в размере расчетной процентной ставки в 8% с оставшейся суммы кредита на начало периода и превышение поступлений Над выплатами идет немедленно на погашение задолженности

Показатели планов поступлений и выплат денежных задолженностей, руб.

Срок выплаты денег	Нетто платежи (без А0)	Выплата денег	Поступление денег	Изменения в денежных средствах		Денежное имущество
		По процентам		Погашение кредита	Формирование актов	Кредит	Активы
t	Nt	It=iVt-1		DVt=Nt+It		Vt=Vt-1+DVt
0	0	0	0	0	0	-126771,59	0
1	28000	-10141,7	0	17858,27	28000,00	-108913,32	28000,00
2	30000	-8713,07	2240,0	2128,693	32240,00	-87626,39	60240,00
3	35000	-7010,11	4819,2	27989,89	39819,20	-59636,50	100059,20
4	32000	-4770,92	8004,7	27229,08	400014,74	-32407,42	140063,94
5	35000	-2592,59	11205	32407,41	46205,12	-0,01	186269,06

Как следует из таблицы, в конце срока эксплуатация инвестиционного объекта инвестор имеет в своем распоряжении оборотные средства, выступающие конечной стоимостью имущества (КСИ) на сумму 186 269,06 руб. (ее нельзя сравнивать с инвестированной суммой 100 тыс. руб., так как оба эти значения относятся к различным моментам времени). При дисконтировании конечной стоимости имущества на начало планового периода по 8%-ной ставке получаем:

КСИ=186 269,06 • 1,08^-5 = 126 771,59 руб.

Разница между этой суммой и показателем инвестированного капитала в размере 100 тыс. руб. соответствует стоимости капитала, равного 26 771,59 руб. При учете условия реинвестирования при финансировании с привлечением собственных средств инвестиционный объект приносит прирост имущества в денежной форме в размере 26 771,59 руб. в момент t= 0, т.е. конечная стоимость имущества составляет:

КСИ=100 000 • 1,08⁵ = 146 932,81 руб.

Разница между значениями КСИ при реализации объекта А и при инвестировании по расчетной процентной ставке составляет 39 336,25 руб. Дисконтируя эту сумму на момент t= 0, получаем разницу в стоимости имущества, равную 26 771,59 руб., соответствующую стоимости капитала:

39 336.25 • 1,08^-5= 26 771,59 руб.

Это также свидетельствует о том, что в модели определения стоимости капитала при оценке абсолютной выгодности в неявной форме производятся сопоставление с инвестированием по расчетной ставке процента. Это вложение капитала представляет собой альтернативу отказа от реальных инвестиций.

По относительной выгодности объектов А и В следует отметить:

а) в объект В можно инвестировать меньше капитала (60 тыс. руб. вместо 100 тыс, руб. в объект А); б) его срок эксплуатации на один год меньше (4 года); в) есть возможность совмещенных инвестиций.

Интересно исследовать, как значения стоимости капитала, считанные из платежных рядов отдельных инвестиционных объектов, подходят для оценки относительной выгоды, если есть различия в затратах капитала на начало эксплуатации (выплаты приобретение) и в период срока эксплуатации, а также в сроках эксплуатации сравниваемых объектов.

Такие исследования между инвестиционными объектами могут не проводиться, если компенсация различий в этих условиях производится посредством вложения (привлечения) финансовых средств, и ее можно не учитывать, так как это не оказывает влияния на выгодность альтернатив, если проценты в будущем начисляются по расчетной ставке процента и стоимость капитала при этом равна нулю. В целом стоимость капитала представляет собой сумму фактических стоимостей выплат на приобретение, притока денежных средств и показателей выручки от ликвидации.

При наличии конкретных данных о будущих инвестиционных объектах метод определения стоимости капитала модифицируется в так называемые инвестиционные цепи (они могут состоять из одинаковых или различных объектов и относиться к разным периодам —конечные или бесконечные инвестиционные цепи).

При оценке метода определения стоимости капитала необходимо учитывать следующие факторы:

а) затраты на вычисления (но они малы из-за необходимости проведения относительно несложных арифметических действий);

б) затраты на сбор данных (заметим, что все методы принятия решений трудоемки, так как требуется подготовка ряда прогнозов по всем моделям инвестиционных расчетов, а в данной модели определения стоимости капитала нужно спрогнозировать выплаты на приобретение, компоненты притока денежных средств в будущем, расчетную процентную ставку, срок эксплуатации и выручку от ликвидации в конце этого срока);

в) принятые в модели допущения (наличие лишь одной целевой функции - стоимости капитала; заданный срок эксплуатации; надежность данных; принадлежность платежей к определенным моментам времени; существование совершенного рынка капитала; начисление процентов на будущие инвестиции по расчетной процентной ставке и вложение высвобождающихся средств; существование значимых решений относительно других инвестиций в других сферах функционирования предприятия и связанная с этим принадлежность платежей к отдельным инвестиционным объектам). Относительно указанных допущений следует отметить следующее.

При принятии решений в инвестиционной сфере обычно приходится учитывать не одну, а несколько целевых функций, поэтому их можно учитывать вне процесса расчета стоимости капитала или применять модели принятия многоцелевых решений.

Срок эксплуатации устанавливается при анализе выгодности до начала применения метода определения стоимости капитала, при этом можно определить оптимальный срок эксплуатации, если только он не задан заранее посредством правовых или технических условий.

Решения относительно других видов реализуемых объектов инвестирования в смежных с ними сферах (производстве, финансировании, сбыте, закупках и т.п.) оказывают влияние на выгодность инвестиционных объектов, учитываемых обычно в форме заданных величин, влияющих на характер динамики поступлений денежных средств и платежей. При отсутствии данных о принадлежности поступлений или одинаковых величинах этих показателей для оценки выгодности можно определять фактическую стоимость выплат или производить учет фактических издержек. При низкой надежности исходных данных можно использовать методы инвестиционных расчетов в условиях неопределенности.

Если сроки платежей составляют менее одного года, то проценты следует начислять чаще, но в этой ситуации возрастают затраты на прогнозирование и расчеты, хотя можно производить и непрерывное начисление процентов (постоянное, моментальное начисление).

Допущение о вложении высвобождающихся средств, а также компенсации разницы в затратах капитала и сроках эксплуатации вложений или будущих инвестиций с начислением на них процентов по единой процентной ставке рассматривалось в решенном выше примере определения стоимости капитала и не соответствует реальной действительности, в которой существует неопределенность относительно инвестиционных возможностей в будущем.

Проблематично также допущение о совершенном рынке капитала, на котором финансовые средства имеются в любом объеме и в любой момент могут быть привлечены или вложены по единой расчетной процентной ставке: в реальности процентные ставки при инвестировании и заимствовании существенно отличаются друг от друга, составляя основу банковской прибыли, и важно определить наиболее подходящий размер этой ставки, влияющей как на сравнимость альтернатив, так и на инвестиционные возможности в настоящем и будущем. При ее расчете можно использовать средневзвешенную величину издержек собственного и заемного капитала, средний показатель долгосрочной рентабельности, а также дифференцированные ставки по вложению и привлечению финансовых средств и получаемые величины реальных доходов и расходов.

2. Метод аннуитетов аналогичен методу определения стоимости капитала при использовании в качестве целевой функции аннуитета, под которым понимаются: а) последовательность платежей одинаковой величины, которые производятся в каждый период рассматриваемого интервала времени; б) сумма, которую инвестор может изымать в каждый период при осуществлении какого-либо проекта. Аннуитет инвестиционного объекта эквивалентен стоимости капитала того же объекта; они преобразуются друг в друга по правилам финансовой математики следующим образом:

где Ann —аннуитет, СК — стоимость капитала. I- расчетная процентная ставка, К_вос - коэффициент восстановления, КСИ — конечная стоимость имущества.

Для метода аннуитетов действуют следующие правила выгодности: инвестиционный объект абсолютно (относительно) выгоден, если его аннуитет выше нуля (выше, чем у любого другого предлагаемого на выбор объекта).

При вычислении аннуитета платежи, представленные в определенной последовательности, обычно относятся к концу периода, причем в качестве интервала времени всегда выбирается срок эксплуатации объекта. Рассмотрим это положение на следующем примере.

Пример 3. Пусть в качестве исходных данных рассматриваются данные табл. 6 примера 6. Определить аннуитеты и выгодность инвестиционных объектов А и В.

Решение. Для альтернативных объектов А и В имеем следующие значения аннуитетов:

Апп_А = 26 771,59 • 1,08⁵ -0.08 / (1,08⁵ -1) = 6 705.12 руб.;

Апп_В = 25 469.32 • 1.08⁴ • 0.08 / (1.08⁴ -1) = 7 689.72 руб.

Так как оба объекта (А и В) имеют положительный аннуитет, то они абсолютно выгодны. При оценке относительной выгодности нужно учитывать, что аннуитеты относятся к разным срокам эксплуатации объектов, охватывая различное число платежей. В нашем случае аннуитет объекта В выше аннуитета объекта А, т.е. Апп_В > Апп_А, однако объект В имеет более короткий срок эксплуатации (поэтому метод аннуитета здесь можно применять лишь в порядке исключения); если же объект с более длительным сроком эксплуатации имеет также более высокое значение аннуитета, то он, несомненно, является относительно выгодным.

Если исходить из возможности осуществления в будущем инвестиций, приносящих проценты по расчетной процентной ставке, то вместо метода аннуитетов следует применять метод определения стоимости капитала. Если же исходить из бесконечного числа идентичных повторений реализации объектов инвестирования, то следует эти методы применять совместно, вычисляя фактическую стоимость, или стоимость капитала постоянной ренты, определяемую как СК = Ann/i.

Подставив, например, рассчитанные выше значения аннуитетов в эту формулу, получим:

СК_А= 6 705,12 / 0,08 = 83 814 руб.;

СК_В= 7 689,72 / 0,08 = 96 121,50 руб.

Таким образом, в данной ситуации инвестиционный объект В является относительно выгодным.

В целом оценка метода аннуитетов совпадает с оценкой определения стоимости капитала, принятыми допущениями и правилами оценки выгодности инвестиционных объектов. Аннуитет - отнесенная к определенным периодам величина, представляющая собой особую форму «средней прибыли».

3. Метод определения внутренней процентной ставки аналогичен методу определения стоимости капитала (СК), отличие состоит в компенсации различий в затратах и сроках эксплуатации, а также в применении иной целевой функции — внутренней процентной ставки (ВПС) r, которая в качестве расчетной процентной ставки обеспечивает нулевое значение стоимости капитала:

(3.41.)

В данном методе определения ВПС используются следующие правила выгодности: инвестиционный объект абсолютно (относительно) выгоден, если его ВПС выше расчетной ставки процента (выше, чем у любого другого предлагаемого на выбор объекта).

Соотношение между результатами определения СК и ВПС зависит от платежного ряда и вида инвестиций. Можно выделить, например, изолированно осуществляемые инвестиции, имеющие место в том случае, если превышение поступлений над выплатами на протяжении всего планового периода направляется исключительно на выплату процентов (по ВПС) и на амортизацию затраченного капитала. А это означает, что в плановый период капитал не реинвестируется (инвестирование происходит изолированно, а ВПС не зависит от процентной ставки, по которой могут быть вложены высвобождающиеся средства).

При изолированно осуществляемом инвестировании (инвестиции, платежный ряд которых имеет только однократное чередование знака) стоимость предназначенного для инвестиций имущества, рассчитанная на основе ВПС, в любой момент планового периода меньше или равна нулю. Это соответствует действительности, если: а) сумма всех нетто-платежей больше или равна нулю; б) сумма всех приходящихся на моменты времени t=0,1,..., Т^* нетто-платежей всякий раз меньше или равна нулю (Т^*- момент времени, на который приходится последнее превышение выплат над поступлениями), т.е.

а) б) для t=0,1,..., Т^*

Динамика стоимости капитала в зависимости от расчетной процентной ставки для двух изолированно осуществляемых инвестиций А и В (рис. 3.2,а) показывает, что результаты методов определения СК и ВПС в отношении абсолютной выгодности совпадают, т.е. стоимость капитала всегда положительна, если ВПС превышает расчетную процентную ставку (i).

При сравнении же относительной выгодности альтернатив инвестиций А и В могут получиться разные по сравнению с методом определения стоимости капитала оценки (на рис. 3.2,а согласно методу определения стоимости капитала следовало бы выбрать объект А, так как СК_А> CK_В, а по методу определения ВПС - объект В, так как r_В > r_А). Какой же объект инвестирования относительно более выгоден?

В данной ситуации метод определения ВПС можно использовать для оценки не относительной выгодности предлагаемых на выбор объектов инвестирования, а для определения разницы в инвестициях. Так, из рис. 3.2,а следует, что ВПС инвестиций для определения разницы соответствует точке r_D, при которой СК_А= СК_В, и r_D > i, если стоимость капитала объекта А с более высокими затратами на приобретение будет также более высокой. При этом применяется следующее правило оценки выгодности: инвестиционный объект А является относительно выгодным по сравнению с объектом В, если ВПС инвестиции для определения разницы выше расчетной ставки процента (т.е. r_D > i). Если же ВПС r_D £ 0, то объект В считают относительно выгодным при всех i> 0.

При комплексных (неизолированно осуществляемых) инвестициях могут быть как несколько положительных процентных ставок, так их может и не быть вообще. В этом случае используют методы приблизительного вычисления ВПС, например, метод интер(экстра)поляции. При этом сначала определяется стоимость капитала СК₁ для процентной ставки i₁. Если эта стоимость положительна (отрицательна), то выбирается более высокая (более низкая) ставка i₂, для которой также вычисляется СК₂. Процентные ставки с соответствующими им показателями стоимости капитала можно использовать для примерного расчета ВПС. Далее осуществляется интерполяция (если один из СК_i> 0, а другой CK_j < 0) или экстраполяция (если оба показателя СК имеют одинаковые знаки). Формула интер(экстра)поляции базируется на теореме об отрезках, по которой рассчитывается ВПС (рис. 2,б). Она имеет следующий вид:

откуда получаем:

Точность полученного приблизительного решения зависит от интервала между значениями процентных ставок i₂ и i₁, а также от отклонений значений КС₁ и КC₂ от нуля. Для получения более точного решения могут потребоваться несколько ВПС.

Возможности метода определения ВПС связаны как с оценкой выгодности инвестиционных объектов, так и с расчетом фактического процента по операциям в сфере финансирования. ВПС. платежного ряда i-ro объекта финансирования представляет собой ставку фактического начисления процентов на него. Рассмотрим это на примере.

Стоимость капитала

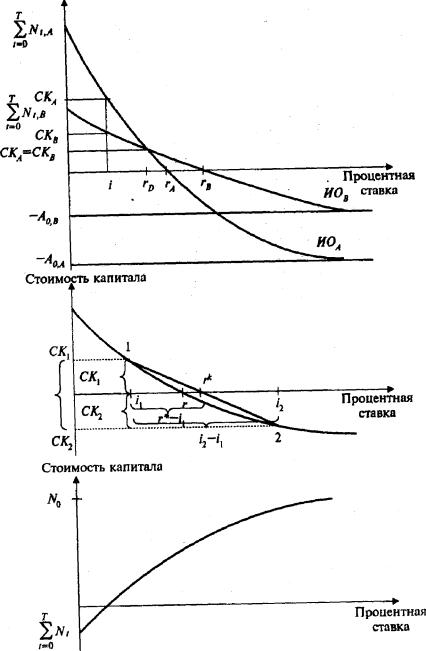
Рис 2. Динамика стоимости капитала в зависимости от расчетной процентной ставки при изолированно осуществляемых инвестициях (а, в) и интерполяция для определения внутренней процентной ставки (б)

Пример 4. Пусть в качестве исходных данных используются данные табл. 3.6. примера 6. Определить ВПС методом интерполяции и выгодность инвестиционных объектов А и В.

Решение. Как было рассчитано ранее в примере 6, стоимость капитала объекта А при процентной ставке i₁= 8% составляет CK_Ai = 26 771,59 руб. Пусть в качестве второй процентной ставки возьмем i₂ = 18%. Тогда получим, что СК_A2 = -1 619,51 руб.:

= -100000+28000×1,18^-1 + 30000 ×1,18 ^-2 + 35000 • 1.18 ^-3 + 32000×l,18 ^-4 + 5000 ×1,18 ^-5 = -1619,51 руб.

Так как разница между ВПС i₁ и i₂ слишком велика, то для более точного решения возьмем i₁ = 17%, при которой имеем, что в этом случае CK _A1= 740,69 руб. Подставив эти значения в формулу интерполяции для r, получим:

r_A= 0,17+740,69/(740,69 -(-1619,51))×(0,18 - 0,17) = 0,1731, или 17,31%.

Таким образом, r_A = 17,31% > i = 8%, то данная альтернатива абсолютно выгодна.

Для инвестиционного объекта В можно также рассчитать примерное значение ВПС. Если при интерполяции ставок взять 25% и 26%, то получим r_B = 25,04%. Таким образом, инвестиционный объект В как абсолютно, так и относительно выгоден.

Пример 5. Предприятие берет кредит в размере 400 тыс. руб. сроком на четыре года, платежи по процентам производятся ежегодно по ставке 9%, а погашение задолженности - в конце срока действия кредита. Оплата осуществляется с 6%-ным дисконтом в начале рассматриваемого интервала времени. Необходимо рассчитать размер ВПС и определить размер фактического процента для объекта финансирования.

Решение. Согласно условиям задачи платежный ряд объекта финансирования имеет вид:

376 000 -36 000 -36 000 -36 000 -436 000

0 1 2 3 4 t

Рис. 3. Платежный ряд объекта финансирования

При 10%-ной ставке i_t стоимость капитала CK₁= -11320,54руб. Так как стоимость капитала при 10%-ной ставке отрицательна (рис. 3.2,в), то можно предположить, что размер ВПС будет выше 10%. При i₂ =11% стоимость капитала составит: СК₂ = 819,57 руб. Используя для интерполяции следующие формулы, получим:

= 0,10+(-11320,54• (0,11-0,10)/ (-11320,54 - -819,57) = 0,1093, или r= 10,93%.

При оценке метода определения ВПС, как и при методе определения капитала, требуются одни и те же данные и допущения, за исключением условия рефинансирования и различий в затратах капитала и сроке эксплуатации. Его не следует применять для оценки абсолютной выгодности, если имеют место комплексные инвестиции, и относительной выгодности на основе сравнения ВПС отдельных объектов. Вместо этого следует проанализировать инвестиции для определения разницы: если это изолированно осуществляемые инвестиции, то на основе сравнения ВПС с расчетной можно оценивать сравнение выгодности; если это комплексные инвестиции, то метод определения внутренней процентной ставки применять не следует для оценки выгодности. В целом ВПС можно рассматривать как критическую процентную ставку для определения абсолютной выгодности инвестиционных альтернатив в сочетании с методом определения капитала при условии ненадежных данных.

4. Метод динамических амортизационных расчетов в рамках модели определения стоимости капитала позволяет определить срок амортизации — период времени, за который инвестируемый капитал восстанавливается благодаря превышению поступлений от эксплуатации объекта над выплатами.

Правило определения выгодности инвестиционных объектов гласит: инвестиционный объект абсолютно (относительно) выгоден, если срок его амортизации ниже заранее заданной предельной величины (ниже подобного показателя любого другого представленного на выбор объекта).

Определение динамического срока амортизации проводится путем поэтапного вычисления кумулированной (суммарной) фактической стоимости нетто-платежей для каждого периода срока эксплуатации, начиная с первого периода, причем пока значение этого показателя отрицательно, срок амортизации еще не достигнут; если же он становится равным нулю (больше нуля), то срок амортизации достигнут (превышен). Путем интерполяции можно примерно определить время, требуемое для амортизации, а также срок амортизации.

Пример 6. Исходные данные соответствуют табл. 3.6. примера 6. Провести поэтапный расчет динамического амортизационного срока эксплуатации для инвестиционных объектов А и В.

Решение. Сведем в табл. 3.8. заданные нетто-платежи для инвестиционного объекта А по пяти моментам времени, а также вычисленные по соответствующим формулам их фактическую стоимость и кумулированную фактическую стоимость нетто-платежей. Из выполненных расчетов видно, что срок амортизации для объекта А превышен в течение четырех периодов (кумулятивная фактическая стоимость объекта А впервые становится больше нуля).

Относительное точное значение срока амортизации (СА) объекта А можно определить с помощью следующей формулы интерполяции:

где - период, в который последний раз кумулированная фактическая стоимость меньше нуля.

Таким образом, для инвестиционного объекта А динамический срок эксплуатации составляет:

3 + (-20 569,77) / (-20 569,77 - 2 951,19) = 3,87 года.

Проведенный расчет для объекта В показал, что его динамический срок амортизации составляет около 2,78 года. Отсюда следует, что объект В относительно выгоден по сравнению с объектом A. Если заданная предельная величина составляет, к примеру, четыре года, то оба объекта можно характеризовать как абсолютно выгодные.

Расчет динамического срока амортизации инвестиционного объекта А

Момент времени t	Нетто-платежи Nt ,py6.	Фактическая стоимость объектов (ФC) руб.	Кумулятивная ФС руб.
0	-100000	-100000	-100000
1	28000	25925,93	-74074,07
2	30000	25720,17	-48353,90
3	35000	27784,13	-20569,77
4	32000	23520,96	2951.19

В целом динамические амортизационные расчеты следует проводить лишь в качестве дополнительного метода включения фактора неопределенности, касающегося определения срока эксплуатации.