Применение математических
методов
в финансовых вычислениях
1. Основные положения
В процессе взаимного обмена
национальных валют устанавливается их курс, представляющий собой цену денежных
единиц одной страны, выраженную в денежных единицах другой страны. Само
определение курса валют называется их
котировкой. Полная котировка предполагает определение курса покупателя
(покупки) и курса продавца (продажи), согласно которым банки покупают и продают
валюту. Единица низшего разряда установленной котировки называется пунктом.
Курс
валют в зависимости от формы его выражения называется обменным или девизным.
Обменный курс показывает, сколько единиц отечественной валюты можно получить в
обмен на единицу иностранной. т.е. это цена иностранной валюты, выраженная в
единицах отечественной валюты. Девизный курс,
являясь обратной величиной к обменному, показывает, сколько единиц
иностранной валюты можно получить за единицу отечественной, т.е. это цена
отечественной валюты, выраженная в единицах иностранной валюты. Определение
обменного курса также называют прямой котировкой, а девизного курса - косвенной
котировкой.
Кроме
обменного и девизного используются также и кросс курсы валют, представляющие
собой соотношения между двумя валютами, следующие из их курсов по отношению к некоторой третьей валюте.
Девизы называются конвертируемыми, если есть
возможность их свободного обмена (конверсии) на валюту других стран по
действующему курсу.
Финансовая
операция, связанная с инвестированием
денежных средств в валюте, в общем виде представляет собой последовательность
следующих действий: конвертирование средств в другую валюту; размещение на
рынках финансовых инструментов полученных средств на некоторый срок;
обратная конвертация средств, полученных от инвестирования, в исходную (или
иную) валюту.
2. Конверсия валюты и
начисление процентов
Рассмотрим совмещение
конверсии (обмена) валюты и наращение простых процентов, сравним результаты от непосредственного размещения имеющихся
денежных средств в депозиты или после
предварительного обмена на другую валюту. При этом возможны следующие 4 варианта
наращения процентов:
1. Без конверсии, когда
валютные средства размещаются в качестве валютного депозита, наращение
первоначальной суммы производится по валютной ставке путем прямого применения
формулы простых процентов.
2. С конверсией, при этом валютные
средства конвертируются в рубли, наращение идет по рублевой ставке, в конце
операции рублевая сумма конвертируется обратно в исходную валюту.
3. Без конверсии, в этом
случае рублевая сумма размещается в виде рублевого депозита, на который
начисляются проценты по рублевой ставке по формуле простых процентов.
4. С конверсией, когда
рублевая сумма конвертируется в какую-либо конкретную валюту и инвестируется в
валютный депозит. Проценты начисляются по валютной ставке. Наращенная сумма в
конце операции вновь конвертируется в рубли.
Операции без конверсии не
представляют сложности. В операции наращения с двойной конверсией имеются два
источника дохода: начисление процента и изменение обменного курса. Причем
начисление процента является безусловным источником (ставка фиксирована, инфляцию не рассматриваем). Изменение обменного
курса может быть как источником дополнительного дохода, так и приводить к
потерям. Остановимся на двух вариантах, предусматривающих двойную конверсию
(варианты 2 и 4).
Введем обозначения:
Рv - сумма депозита в валюте,
Рr - сумма депозита в рублях,
Sv - наращенная сумма в валюте,
Sr - наращенная сумма в рублях,
К0 - курс обмена в начале операции (курс валюты в руб.),
K1 -
курс обмена в конце операции,
п - срок депозита,
i -
ставка наращения для рублевых сумм (в виде десятичной дроби),
j -
ставка наращения для конкретной валюты.
Рассмотрим вариант:
ВАЛЮТА=> РУБЛИ => РУБЛИ => ВАЛЮТА.
Операция состоит из трех
этапов: обмена валюты на рубли, наращения рублевой суммы, обратное
конвертирование рублевой суммы в исходную валюту. Наращенная сумма, получаемая
в конце операции в валюте, составит
Sv = Pv K0 (1 + ni) / K1 (1)
Как видим, три этапа
операции нашли свое отражение в этой формуле в виде трех сомножителей.
Множитель наращения с учетом двойного
конвертирования равен
![]() (2)
(2)
где k=K1 /K0 - темп роста обменного курса за срок операции. Из (2)
следует, что множитель наращения т связан
линейной зависимостью со ставкой i и
обратной с обменным курсом в конце операции K1 (или с темпом роста
обменного курса k).
Исследуем зависимость общей доходности операции с
двойной конверсией от соотношения конечного и начального курсов обмена k.
Простая годовая ставка процентов, характеризующая
доходность операции, равна
![]()
Подставим
в эту формулу выражение для Sv
![]() (3)
(3)
Из (3) следует, что с увеличением k доходность iэфф падает по гиперболе с асимптотой
1/п. При k=1
доходность операции равна рублевой ставке, т.е. iэфф = i. При k > 1 iэфф < i, а при k < 1 iэфф >i.
При некотором критическом значении k, которое обозначим как k*, доходность операции равна
нулю. Из равенства iэфф = 0
находим
k* = 1+ ni, (4)
что
означает
K*1 =Ko (1+ ni). (5)
Таким
образом, если ожидаемые величины k
или К*1 превышают свои критические
значения, то операция убыточна (iэфф < 0).
Определим максимально
допустимое значение курса обмена в конце операции K1, при котором эффективность
будет равна существующей ставке по депозитам в валюте, и применение двойного
конвертирования не дает никакой дополнительной выгоды. Для этого приравняем
множители наращения для двух альтернативных операций
1 + nj = (1 + ni) Ко / K1.
Из равенства следует, что
max К1 = Ко (1 + ni) / (1 + nj) (6)
или
max k = K 1
/ K0 = (1 + ni) / (1 + nj) (7)
Таким образом, депозит
валюты через конверсию в рубли выгоднее валютного депозита, если обменный курс
в конце операции ожидается меньше max K1.
Рассмотрим вариант:
РУБЛИ => ВАЛЮТА => ВАЛЮТА ==> РУБЛИ.
Это операция с двойной
конверсией, когда исходная и конечная суммы в рублях. В этом случае трем этапам
операции соответствуют три сомножителя для наращенной суммы
![]() (8)
(8)
Проведем анализ
эффективности этой операции и определим критические точки.
Доходность операции в целом определяется по формуле
![]()
Отсюда, подставив выражение для Sr ,
получим
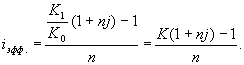 (9)
(9)
Зависимость показателя
эффективности iэфф от k линейная,
при k = 1 iэфф = j,
при k > 1 iэфф >j,
при k < 1 iэфф < j.
Найдем критическое значение k*,
при которых iэфф = 0:
k* = 1/ (1 + nj) или
К*1 =K0 / (1 + nj). (10)
Таким образом, если ожидаемые величины k или K1 меньше своих критических
значений, то операция убыточна (iэфф < 0).
Минимально допустимая
величина k (темпа роста валютного
курса за весь срок операции), обеспечивающая такую же доходность, что и прямой
вклад в рублях, определяется путем приравнивания множителей наращения для
альтернативных операций (или из равенства iэфф = i).
К1 (1 + nj) / K0 = 1 + ni,
откуда
min k = (1 + ni) / (1 + nj) или min К1 = К0 (1 + ni) / (1 + nj). (11)
Таким образом, депозит рублевых
сумм через конверсию в валюту выгоднее рублевого депозита, если обменный курс в
конце операции ожидается больше min K1.
Рассмотрим вариант
совмещения конверсии валюты и наращение сложных процентов.
ВАЛЮТА => РУБЛИ => РУБЛИ =>ВАЛЮТА.
Три этапа операции запишем в одной формуле для наращенной суммы
Sv = PvK0 (1 + i)n / K1 (12)
где
i - ставка сложных процентов.
Множитель наращения
m = (1 + i)n K0 / K1 = (1 + i)n / k, (13)
где k = K1 /K0 - темп роста валютного курса за период операции.
Определим доходность
операции в виде годовой ставки сложных процентов iэ. Из формулы наращения по
сложным процентам
S = P (1+ i)n
находим 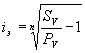
Подставив в эту формулу значение Sv , получим
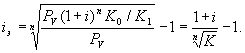 (14)
(14)
Из этого выражения следует,
что с увеличением темпа роста k
эффективность iэ падает.
Анализ показывает, что при k = 1
iэ = i, при k >1 iэ < i, а при k < 1 iэ >i. Критическое
значение k, при котором эффективность
операции равна нулю, определяется как
k* = (1+ i)n, (15)
что
означает равенство среднегодового темпа роста курса валюты годовому темпу
наращения по рублевой ставке.
Таким образом, если
ожидаемые величины k или K1 больше своих критических значений, то
рассматриваемая операция с двойной конверсией убыточна (iэ < 0).
Максимально допустимое
значение k,
при котором доходность oneрации будет равна доходности
при прямом инвестировании валютных средств по ставке j, находится из равенства
соответствующих множителей наращения:
(1+ j)n = (1+ i)n / kmax,
откуда
kmax = (1+ i)n / (1+ j)n
max K1 = K0 (1+ i)n
/ (1+ j)n. (16)
Таким
образом, депозит валюты через конверсию в рубли выгоднее валютного депозита,
если обменный курс в конце операции ожидается меньше max K1.
Пример 1.
Имеется сумма в
долларах, которую предполагается разместить на полугодовой депозит. Обменный
курс в начале операции 34 р. за доллар, в конце операции предполагается 35 р.
Годовая ставка простых процентов по рублевым депозитам 12%, по валютным 5%.
Как выгоднее разместить
вклад, как валютный или через конверсию в рублях?
Решение.
При двойной конверсии: доллар Þ рубли Þ рубли Þ доллар расчет производим по формуле (3) с учетом того, что k = K 1 / K0,, где
k – темп роста обменного курса за срок операции,
K0 – курс обмена в начале операции,
K 1 –
курс обмена в конце операции.
k = K 1 / K0 = 35 / 34 = 1,029.
iэ = [(1 + 0,5 × 0,12) / 1,029 × 0,5] - 1 / 0,5
= 0,06.
Ответ.
По условию задачи, доходность валютного депозита 5%, доходность операции с двойной конверсией 6%. Следовательно, выгоднее разместить вклад рублевый.
Пример
2. В обменном пункте установлена следующая
котировка американского доллара к рублю;
покупка – 29 руб., продажа 29,8 руб.
Определите:
а)
сколько рублей будет получено при обмене 350 долларов;
б)
какое количество американских долларов можно приобрести на 4500 евро.
Решение:
а)
Для перевода суммы в иностранной валюте в эквивалентную ей сумму в национальной
валюте необходимо умножить ее на курс покупки:
350×29=10150
руб.
б)
Для перевода суммы в национальной валюте в эквивалентную ей сумму в иностранной
валюте необходимо ее разделить на курс продажи:
![]() доллар
доллар
Пример
3. В банке установлена следующая котировка валют:
|
|
Покупка |
Продажа |
|
Доллар
США/руб |
28,50 |
29,40 |
|
Евро/руб. |
34,00 |
34,80 |
Определите:
а)
кросс-курс доллара США к евро;
б)
сколько долларов США можно приобрести на 3500 евро.
Решение:
а)
Рассмотрим операцию обмена долларов на евро.
В
начале доллары обменяем на рубли по курсу покупки/доллара США=28,50 руб., а
затем полученная сумма обменивается на евро по курсу продажи евро= 34,80 руб.,
т.е. 1 руб.= 1/34,80 евро.
Таким
образом, 1 доллар США = 28,50 ×1/34,80=
0,82 евро.
Делаем
вывод, что в этом банке кросс-курс покупки доллара США к евро равен 0,82 евро
за один доллар.
Рассмотрим
операцию обмена евро на доллары.
В
начале евро обмениваются на рубли по курсу покупки 1 евро = 34,00, т.е. 1 руб=1/34
евро, а затем полученна я сумма обменивается на доллары по курсу продажи 1
долл. США= 29,4 руб., т.е. 1 доллар= 29,4×1/34=0,8647
евро. Следовательно в этом банке кросс-курс продажи доллара США к евро равен
0,8647 евро за доллар.
б)
Чтобы определить сколько долларов США можно приобрести на 3500 евро, поменяем
евро на рубли по курсу покупки евро=34 руб., затем полученная сумма
обменивается на доллары по курсу продажи доллара =29,4 руб., т.е. ![]() долл.
долл.
Этот
же результат можно получить, если поделим 3500 евро на 0,8647 (кросс-курс
продажи доллара к евро);
3500/0,8647=4047,65
долл.
Незначительное
расхождение получено за счет округления.