Формулы современной величины

1. Обычная годовая рента.

Пусть член годовой ренты равен R, процентная ставка i, проценты начисляются один раз в конце года, срок ренты п. Тогда дисконтированная величина первого платежа равна

где

v = 1/(1 + i) - дисконтный множитель.

Приведенная к началу ренты величина второго платежа равна Rv² и т.д. Таким образом, приведенные величины образуют геометрическую прогрессию:

Rv, Rv², Rv³, ... , Rvⁿ,

сумма членов которой является современной величиной

(1)

где

, (2)

a_n;i - коэффициент приведения ренты.

Коэффициент приведения ренты зависит только от двух параметров: срока ренты п и процентной ставки i, ее значения имеются в таблице.

Современная величина ренты пренумерандо равна

(3)

2. Рента p-срочная, р ³ 1, m ³ 1.

Аналогично можно получить формулу для расчета современной величины ренты в общем случае для произвольных значений p и m.

(4)

Современная величина ренты пренумерандо

(5.)

Пример.

Владельцы химического завода предложили администрации города в качестве компенсации за ущерб, нанесенный окружающей среде, выплатить 500 тыс. дол. в течение 5 лет полугодовыми равными платежами. Найти современную величину вносимой ренты при ежеквартальном дисконтировании платежей сложными процентами по годовой процентной ставке 20%.

Решение.

По формуле (4) найдем современную величину вносимой ренты:

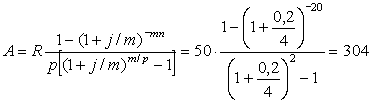тыс.дол.

Ответ. Современная величина ренты составит 304 тыс. дол.