Формулы наращенной
суммы
Рассмотрим наращение для
различных случаев начисления рент.
1. Обычная годовая
рента.
Пусть в конце каждого года в течение п лет на расчетный счет вносится по R рублей, проценты
начисляются один раз в год по ставке i. В
этом случае первый взнос к концу срока ренты
возрастет до величины 
так как на сумму R проценты начислялись в течение (п - 1)
года. Второй взнос увеличится до 
и т.д. На последний взнос проценты не начисляются.
Таким образом, в конце срока ренты ее наращенная сумма будет равна сумме членов
геометрической прогрессии
в которой первый член равен R,
знаменатель (1+ i),
число членов п. Эта сумма равна
(1)
где
(2)
называется коэффициентом
наращения ренты. Он зависит
только от срока ренты п и уровня процентной ставки i.
Наращенная сумма ренты пренумерандо в (1 + i) раз
больше постнумерандо и при m= p =1
(3)
Пример 1.
Для создания пенсионного фонда в банк
ежегодно выплачивается рента постнумерандо в размере 10 млн. р.. На
поступающие платежи начисляются проценты по
сложной годовой ставке 18%. Определить размер фонда через 6 лет.
Решение.
По формуле (1) имеем:
млн. р.
Ответ. Пенсионный фонд через 6 лет
будет составлять 99,42 млн. р.
2. Годовая рента, начисление
процентов m раз в году.
Пусть платежи делают один раз в конце года, а
проценты начисляют т раз в году. Это означает,
что применяется каждый раз ставка j/m,
где j -
номинальная ставка процентов. Тогда члены ренты с начисленными до конца срока
процентами имеют вид
Если прочитать предыдущую строку справа налево, то
получим геометрическую прогрессию,
первый членом которой R, знаменатель (1+ j/m)m, число членов п. Сумма членов этой прогрессии будет
наращенной суммой ренты. Она равна
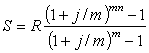(4)
Наращенная сумма ренты пренумерандо вычисляется по формуле
(5)
Пример 2.
В условиях примера 1 принять, что проценты банком начисляются ежеквартально по номинальной ставке 18% годовых. Сделать вывод, какой вариант начисления процентов выгоден кредитору.
Решение.
По формуле (4) имеем
= 97, 45 млн. р.
Ответ. Кредитору выгоден вариант примера 2.2., чтобы на
ренту начислялись проценты ежеквартально, при этом размер фонда будет
составлять 97,45 млн. р.
3. Рента p-срочная, m = 1.
Найдем наращенную сумму при условии, что рента
выплачивается р раз в году равными
платежами, а проценты начисляются один раз в конце года.
Если R -
годовая сумма платежей, то размер отдельного платежа равен R/p.
Тогда последовательность платежей с начисленными до конца срока процентами
также представляет собой геометрическую прогрессию, записанную в обратном
порядке,
у
которой первый член R/p,
знаменатель (1+ i)1/p, общее число членов пр. Тогда наращенная сумма
рассматриваемой ренты равна сумме членов этой геометрической прогрессии
(6)
где
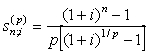(7)
коэффициент наращения
р-срочной ренты при m = 1.
Наращенная сумма ренты пренумерандо вычисляется по формуле:
(8)
Пример 3.
Господин Иванов вносит в банк в конце каждого месяца по 500 р.. На
поступающие суммы платежей начисляются сложные проценты по годовой процентной
ставке 22%. Определить размер
начисленной суммы через 8 лет.
Решение.
По форомуле (6) найдем размер начисленной суммы:
S = 500 [(1 + 0,22)8 - 1] / [(1 + 0,22)1/8 - 1] = 52,806 тыс. р.
Ответ. Размер начисленной банком суммы господину Иванову
через 8 лет составит 52,806 тыс. р.
4. Рента p-срочная, р = т.
В контрактах часто начисление процентов и
поступление платежа совпадают во времени. Таким образом число платежей р в году и число начислений процентов т совпадают, т.е. р = т. Тогда для получения формулы расчета наращенной суммы воспользуемся аналогией с
годовой рентой и одноразовым начислением процентов в конце года, для которой
Различие
будет лишь в том, что все параметры теперь характеризуют ставку и платеж за
период, а не за год. Таким образом, получаем
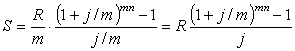(9)
Наращенная сумма ренты пренумерандо вычисляется по
формуле:
(10)
Пример 4.
Господин Петров должен отдать долг в размере 200 тыс. р. Для того, чтобы
собрать эту сумму он планирует в течение 3-х лет в конце каждого полгода
вносить в банк одну и ту же сумму и на нее каждые полгода начисляются сложные
проценты по годовой ставке 15%. Какова должна быть величина вносимых господином
Петровым полугодовых вкладов при полугодовом начислении процентов? Рассмотреть случай, когда в банк вносится
сумма один раз в конце каждого года и начисление процентов производится по той
же сложной процентной ставке.
Решение.
Из (9) найдем сумму (R), которую необходимо вносить в банк
каждые полгода при полугодовом
начислении сложных процентов:
R = S j / [ (1 + j/m)mn - 1] =
200 × 0,15 / [ (1 + 0,15/2)2×3 - 1] = 55,228 тыс. р.
Из формулы (1) найдем сумму, которую необходимо вносить в банк каждый год
при годовом начислении сложных процентов:
R = S j / [ (1 + j)n - 1] = 200 × 0,15 / [ (1 + 0,15)3 - 1] = 57,692 тыс. р.
Ответ. Господину Петрову необходимо
вносить в банк каждые полгода и
полугодовом начислении сложных процентов сумму, равную 55,228 тыс. р. и
сумму в 57,692 тыс. р. при ежегодном вкладе и годовом начислении сложных
процентов. Первый вариант вклада для него более выгоден.
5. Рента р-срочная, p ³ 1 , m ³ 1.
Это самый общий случай р-срочной ренты с начислением процентов т раз в году, причем, возможно р
¹ т.
Первый член ренты R/p,
уплаченный спустя 1/р года после
начала, составит к концу срока вместе с начисленными на него процентами
второй член ренты к концу срока возрастет до
и
т.д. Последний член этой записанной в обратном порядке геометрической
прогрессии равен R/p, ее знаменатель (1+ j/m)m/p,
число членов пp. В
результате получаем наращенную сумму
(11)
Наращенная сумма ренты пренумерандо определяется по формуле:
(12)
Пример 5.
Предприятие создает страховой фонд, для чего направляет в банк платежи в размере
100 тыс. р. в конце каждых 4-х месяцев, начисление сложных процентов банк производит 1 раз в
полгода по годовой ставке 18%. Определить размер страхового фонда через 10 лет.
Решение.
По формуле (11) найдем:
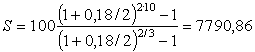тыс.руб.
Ответ. Размер страхового фонда
предприятия через 10 лет составит 7790,86
тыс.р.