Формула наращения по сложным процентам

Пусть первоначальная сумма долга равна Р, тогда через один год сумма долга с присоединенными процентами составит , через 2 года  через п лет -

Таким образом, получаем формулу наращения для сложных процентов

                             (1)

где S - наращенная сумма,

i - годовая ставка сложных процентов,

п - срок ссуды,

 - множитель (коэффициент) наращения, который обозначим Kнар..

В практических расчетах в большинстве случаях применяют дискретные проценты, т.е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, квартал и т.д.).

Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен Р, а знаменатель

Сравним коэффициенты наращения по простым и сложным процентам по ставке 20% годовых и временной базе 360 дней. Результаты расчета поместим в таблицу 1.

Таблица 1.

Коэффициент наращения

30 дней

180 дней

1 год

5 лет

10 лет

1 + ni

1,0167

1,1

1,2

2,0

3,0

(1 + i)n

1,0153

1,0954

1,2

2,4883

6,1917

 

Отметим, что при сроке операции менее года наращение по простым процентам дает больший результат, чем по сложным, а при сроке более года - наоборот.

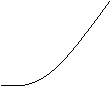
Графически изменения коэффициентов наращения по простым и сложным процентам представлены на рис 1.

                                                                                                        

    Kнар                                                                                              

                                                                                                        

                                                                                                        

1                                                                                                      

                                                                                                        

                                                                                                        

             1                                           n                                            

                                                                                                        

Рис. 1.

В том случае, когда ставка сложных процентов меняется во време­ни, формула наращения имеет следующий вид

                            (2)

где i1, i2, … ik - последовательные значения ставок процентов, действующих в периоды n1, n2,..., nk  соответственно.

   Выражение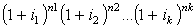–множитель (коэффициент) наращения.

Пример.

В договоре зафиксирована переменная ставка сложных процентов, определяемая как 15% годовых плюс маржа 6% в первые два года, 8% в третий год, 10% в четвертый год. Определить величину множителя наращения за 4 года.

Решение.

Найдем множитель наращения.  (1 + 0,21)2 (1 + 0,23) (1 + 0,25) = 1,83.

Ответ.

Множитель наращения за 4 года составляет 1,83.