Задача. Дана производная функция где y-объем товарной продукции в стоимостном выражении, х₁ – фонд заработной платы, х₂ – стоимость основных фондов. Произошло изменение используемых ресурсов: фонд заработной платы уменьшился на 3%, стоимость основных фондов возросла на 2% .на сколько процентов при этом изменится:

1. объем товарной продукции,

2. производительность труда,

3. фондоотдача.

Решение.

1) Определим изменение объема товарной продукции в процентном выражении. Прологарифмируем производственную функцию.

.

Найдем полный дифференциал от данного выражения:

.

Величины и выражают процентные изменения переменных х₁, и х₂, они соответственно равны -0,03 и 0,02. Величина будет выражать соответствующее процентное изменение переменной у.

.

Следовательно, объем товарной продукции не изменился.

Найдем изменение объема товарной продукции в процентном выражении вторым способом. Исходное значение объема товарной продукции в стоимостном выражении было равно и это составляет 100%. По условию значение х₁ уменьшилось на 3%, т.е. стало 0,97 х₁, а значение х₂ увеличилось на 2%, т.е. стало 1,02х_{2 .} Тогда Найдем, сколько процентов составляет у_н по отношению к у_исх.

у_исх - 100%

у_н - А %

.

Так как А = 100 %, то объем товарной продукции не изменился.

2) Производительность труда является отношением объема товарной продукции к фонду заработной платы . Она была равна и это составляло 100%. При изменении х₁ и х₂ новая производительность труда будет равна . Составим пропорцию:

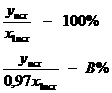
Отсюда

.

Так как В = 103%, то произошло повышение производительности труда на

103% - 100% = 3%.

3) Фондоотдача является отношением объема товарной продукции к стоимости основных фондов . Она была равна и это составляло 100%. При изменении х₁ и х₂ новая производительность труда будет равна . Составим пропорцию:

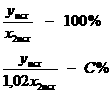
Отсюда

.

Так как С = 98%, то произошло уменьшение фондоотдачи на

100% - 98% = 2%.