Задача. В таблице представлены данные, отражающие динамику продаж на рынке недвижимости по месяцам в течение двух лет. Дать прогноз продаж на глубину в один интервал.


1	11,12	7	12,25	13	7,44	19	8,72
2	11,43	8	9,24	14	8,07	20	7,12
3	12,34	9	11,19	15	6,37	21	8,45
4	10,17	10	8,12	16	5,27	22	7,34
5	9,09	11	5,75	17	6,42	23	8,54
6	11,51	12	7,36	18	5,12	24	10,23

Решение. Выдвинем гипотезу о том, что процесс описывается моделью и рассчитаем ее параметры.

Для регрессионного анализа в Excel есть функции ЛИНЕЙН и ТЕНДЕНЦИЯ, а также процедура Регрессия. Для вызова последней нужно выполнить Сервис Анализ данных и далее в появившемся диалоговом окне в списке Инструменты анализа выбрать строку Регрессия.

В появившемся диалоговым окне следует 1) задать Входной интервал Y, т.е. дать ссылку на столбец зависимых переменных; 2) указать Входной интервал Х, т.е. дать ссылку на область ячеек, содержащих факторные переменные; 3) указать выходной диапазон, т.е. дать ссылку на область ячеек, куда будут выведены результаты. Для этого следует поставить переключатель в позицию Выходной интервал, навести указатель мыши на соответствующее окно, и указать в нем левую верхнюю ячейку выходного диапазона.

Выходной диапазон содержит результаты дисперсионного анализа, коэффициенты регрессии, погрешности.

Пример подготовки исходных данных и результаты представлены соответственно на рис. 1 и рис. 2.

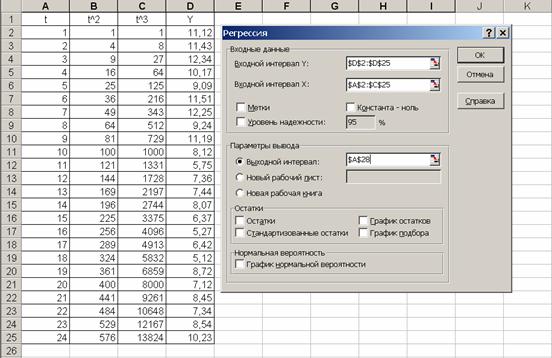
Рис 1. Заполнение диалогового окна Регрессия

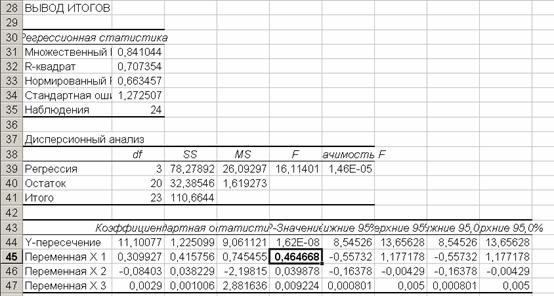
Рис 2. Результаты регрессионного анализа

В разделе Регрессионная статистика содержатся общие показатели. Квадрат коэффициента множественной корреляции (коэффициент детерминации) показывает, какая доля вариации результирующего признака объясняется действием факторов:

= = .

Нормированный коэффициент детерминации отличается от обычного тем, что рассчитывается не по вариациям, а по оценкам соответствующих дисперсий, т.е. с учетом степеней свободы (объема выборки и числа оцениваемых параметров ):

= .

Стандартная ошибка – корень из остаточной дисперсии:

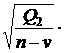
Отношение стандартной ошибки к среднему значению результирующего признака может служить приблизительной оценкой прогнозного качества регрессионной модели. Если в качестве квантиля t-распределения взять 2, то предельную абсолютную погрешность прогноза можно оценить по формуле .

Содержание таблиц результатов в принятых обозначениях:

Дисперсионный анализ
	Df		SS		MS		F			Значим. F
Регрессия
Остаток
Итого

Y-пересечение
Переменная X₁
…		…		…		…		…	…		…
Переменная X_m

Оценка значимости регрессии осуществляется в данном случае не сравнением и , а по показателю, который называется здесь Значимость F, и представляет собой уровень значимости , при котором =. Регрессию следует считать значимой, если < 0,05. Аналогично, только по -критерию, оценивается значимость коэффициентов регрессии.

Границы доверительных интервалов для коэффициентов регрессии определяются для по формулам:

= , = .

Как показывают результаты, в целом регрессия значима, но один из параметров, а именно , незначим: = 0,464668 > 0,05 (выделено жирным шрифтом). Поэтому был сделан расчет модели . Результаты представлены на рис. 3.

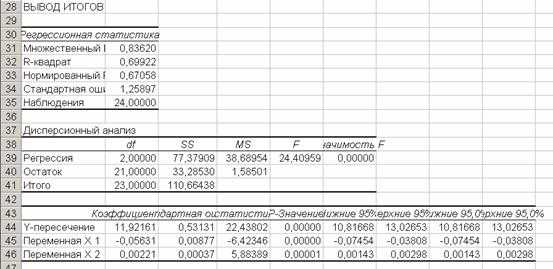
Рис. 3. Результаты регрессионного анализа

Получилась модель 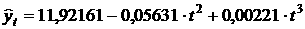, которая обладает высокой значимостью регрессии в целом и каждого параметра в отдельности. Автокорреляции нет: 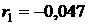. Для вычисления использована процедура Сервис Анализ данных Корреляция (Рис. 4).

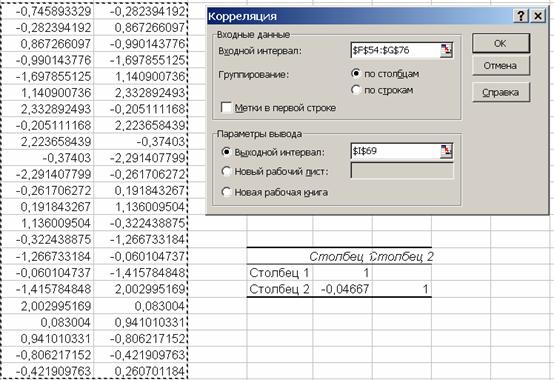
Рис. 4. Диалоговое окно корреляционного анализа

Графическая иллюстрация результатов представлена на рис. 5 (а - исходный временной ряд и тренд; b - остаточный ряд; c - поле автокорреляции остатков для лага = 1).

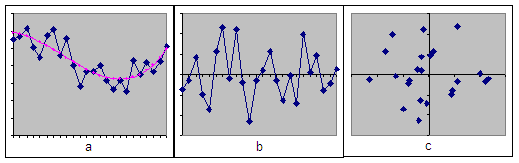
Рис. 5

Прогноз продаж на глубину в один интервал (на двадцать пятый месяц):

= .

Предельная абсолютная погрешность . Следовательно, с практической достоверностью можно утверждать, что объем продаж не выйдет за пределы интервала .