Уравнение Слуцкого

В теории потребительского выбора и функции спроса важное значение имеют уравнения Слуцкого Е.Е., характеризующие количественные зависимости между изменением цен на отдельные товары и доходов потребителей, с одной стороны, и структурой покупательского спроса - с другой.

Наиболее просто основное уравнение Слуцкого формулируется следующим образом:

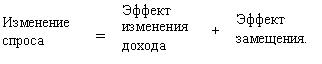
Иными словами, изменение спроса на некоторый товар при повышении или снижении его цены складывается из двух частей. Это влияние непосредственного изменения спроса, т.е. изменения реальной возможности приобретать данный товар в результате изменения цены на него, и косвенного влияния в результате переключения спроса на другие товары.

Рассмотрим функции спроса при неизменной величине функции полезности в точке локального рыночного равновесия:

Нахождение решения , обусловленного изменением только величины цены , равно:

.

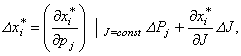
Поделив обе части на и переходя к пределу при , получим:

(*)

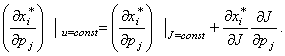Так как то при изменении цены на величину приращение дохода составит:

. (1)

Из этого выражения следует, что

Поскольку дифференциал от функции равен нулю, то имеем соотношение

.

В точке локального равновесия выполняются соотношения проноретональности первых производных функции полезности и соответствующих цен:

Подставив эти соотношения в (1) и сократив на сомножитель , получим

. (2)

Разделим полученное уравнение на и перейдем к пределу при тогда получим

Подставив эти уравнения в (1), придем к формулам

т.е. в точке рыночного равновесия относительное изменение дохода, вызванное изменением цены на товар, равно количеству этого товара. Подставляя эти формулы в (*), получим

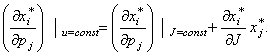
Поскольку в правой части первое слагаемое есть действие эффекта изменения цены при неизменном доходе на компенсационную добавку величины продукта, то это слагаемое называется компенсационным. Перенесем второе слагаемое правой части в другую сторону, получим уравнение Слуцкого:

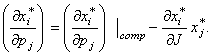(3)

Дадим экономический смысл уравнения Слуцкого. Левая часть уравнения представляет "отклик" точки спроса при неизменном доходе на изменение цены j-го товара. Второе слагаемое правой части описывает действие эффекта дохода: оно представлено произведением, в котором одним из сомножителей является "отклик" точки спроса на изменение дохода, другим - величина спроса на j-й товар. Первое слагаемое правой части (3) показывает, что при изменении цены j-го товара на при неизменных остальных ценах и доходе изменяются точка спроса и максимальная полезность. Изменим доход так, чтобы максимальная полезность имела то же значение, - это и является компенсацией.

Дадим несколько соотношений, которые получаются в процессе вывода уравнения Слуцкого и имеют экономический смысл:

1) Уравнение связывает прежние цены с приращениями товаров, что указывает на изменение спроса. Спрос на одни товары растет, на другие падает.

2) Из уравнений (1) и (3) следует: . Это означает, что при увеличении цен компенсация дохода должна быть положительной, при уменьшении цен - отрицательной.

3)

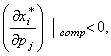(4)

это означает, что при повышении цены спрос на товар падает даже при компенсации дохода.

.

Данное уравнение показывает, что часть слагаемых суммируется со знаком "плюс", а часть со знаком "минус". Товар называется "ценным", если при повышении дохода спрос на него растет, в противном случае товар является малоценным. Из уравнения также следует, что не все слагаемые отрицательны. Положительным слагаемым соответствуют ценные товары. К ценным товарам следует отнести высококачественные (масло, мясо и др.) и предметы роскоши. К малоценным - маргарин, картофель и др. При повышении дохода потребление высокоценного товара возрастает, малоценного - снижается.

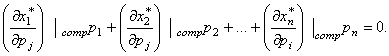
Так как то из неравенства (4) следует, что найдется какой-то j-й товар, для которого

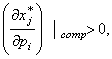
т.е. при повышении цены на i-й товар потребление j-го товара растет при компенсационном изменении дохода J. В этом случае j-й товар называется заменяющим i-й товар. Например, для большинства потребителей при повышении цены на мясо оно может быть заменено на рыбу, сливочное масло - маргарином.

Кривые "доход - потребление", "цена - потребление". Для частного случая двух переменных изменение спроса при изменении дохода и цен можно проиллюстрировать геометрически. Рассмотрим зависимость спроса от дохода при постоянном векторе цен. Предположим, что среди товаров нет малоценных (рис. 1).

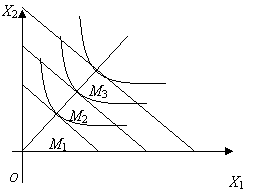
Рис. 1

При увеличении дохода бюджетная линия перемещается параллельно самой себе, а точками оптимума (спроса потребителей) являются точки М₁, М₂, М₃. Линия, соединяющая точки О, М₁, М₂, М₃, является вектором покупательского спроса в зависимости от дохода при заданном векторе цен. Такая линия называется кривой Энгеля, или линией "доход - потребление".

Если товар 1 по сравнению с товаром 2 малоценный, то кривая Энгеля принимает особый вид. На участке СD с отрицательным наклоном кривой спрос на малоценный товар начинает падать. (рис. 3).

		Х1
	О

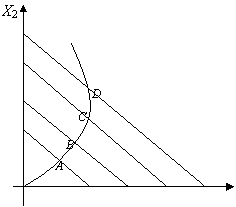
Рис. 2

Предположим, что цена товара 1 меняется. Рассмотрим, как изменяется спрос на товары 1 и 2 (рис. 2).

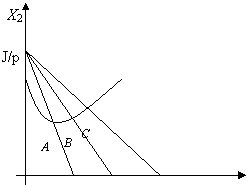
О

Х₁

Рис. 3

Уравнение связи . Пусть р₁ уменьшается, точка J/p₁ переходит в точку , а точка - в точку В, которая является новой точкой равновесия, обеспечивающей потребителю новый . Уменьшим цену , тогда точка перейдет в точку , а точка В - в точку С и т.д. Кривая АВС - линия "цена - потребление". В отличие от линии "доход - потребление" она проходит через точку .