Основные понятия сетевой модели

Сетевая модель - графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа. Сетевой график - это ориентированный граф без контуров. В сетевом моделировании имеются два основных элемента - работа и событие.

Работа - это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.

Фиктивная работа - это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.

Событие - это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.

Путь - это любая непрерывная последовательность (цепь) работ и событий.

Критический путь - это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называются критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.

При построении сетевых моделей необходимо соблюдать следующие правила:

1. Сеть вычерчивается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.

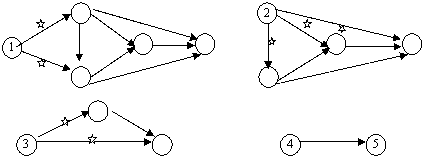
2. Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 1).

Рис. 1 Рис. 2

3. В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит ни одна работа (рис. 1).

1. В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рис. 2).

Рис. 3 Рис. 4

2. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 4). Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. Из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычерчивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Пример нумерации сетевого графика показан на рис. 5.

Рис. 5

Продолжительность выполнения работ устанавливается на основании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором - стохастическими (вероятностными).

Рассмотрим в качестве примера программу создания нового бытового прибора, пользующегося спросом у населения. Необходимые данные приведены в табл. 1.

Таблица 1

Операция

Наименование работы

Непосредственно предшествующие операции

Продолжительность операции, недель

А, Б

В, Г

З, К

Разработка технической документации (ТД) на прибор и его электронную часть

Разработка технологической документации на электронную часть прибора и прибор

Передача ТД на прибор

Изготовление приборов

Изготовление электронной части прибора

Разработка ТД на эксплуатацию прибора и электронную часть

Сборка и испытания прибора

А, Б

Г, Д

В, Г

Е, Ж

А-3, Б-2

В-2, Г-2

З-5, К-2

На основании данных табл. 1 построим сетевой график создания прибора с учетом вышеизложенных рекомендаций (рис. 6).

Рис. 6

Расчет временных параметров сетевого графика

Основным временным параметром сетевого графика является продолжительность критического пути.

Расчет критического пути включает два этапа. Первый называется прямым проходом. Вычисления начинают с исходного события и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события вычисляется одно число, представляющее ранний срок его наступления. На втором этапе, называемом обратным проходом, вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления.

Рассмотрим прямой проход.

t_i^р.н - ранний срок начала всех операций, выходящих из события i.

Если i = 0, то t₀^p^{. н} = 0.

t_j^р.н - ранний срок начала всех операций, входящих в j.

t_j^р.н = max { t_i ^p^.н + t_ij } для всех (i, j),

где t_ij - продолжительность операции (i, j).

Рассмотрим последний пример.

t₁^р.н = t₀^р.н + t_0,1 = 0 + 2 = 2, t₂^р.н = t₀^р.н + t_0,2 = 0 + 3 = 3,

t₃^р.н = max { 2 + 2, 3 + 3 } = 6, t₄^р.н = t₂^р.н + t_2,4 = 3 + 2 = 5,

ⁱ^{= 1,2}

t₅^р.н = max { 6 + 3, 5 + 7 } = 12, t₆^р.н = max { 6 + 2, 12 + 6, 5 + 5 } = 18.

ⁱ^{= 3,4}ⁱ^{= 3,4,5}

Найдем t_ij^p^.^o - ранний срок окончания работы. Он является наиболее ранним (минимальным) из возможных моментов окончания работы при заданной продолжительности работ:

t_ij^p^.^o = t_i^p^.н + t_ij.

Результаты расчетов занесем в табл. 2.

Прямой проход закончился, начинаем обратный.

t_i^п.о - поздний срок окончания всех операций, входящих в событие i.

Если i = n, где n - завершающее событие сети, то t_n^п.о = t_n^р.н и является отправной точкой обратного прохода. Поэтому t₆^п.о = t₆^р.н= 18.

t_i^п.о = min { t_j^п.о - t_i_,_j } - для всех операций (i, j),

t₆^п.о = t₆^р.н = 18, t₅^п.о = t₆^п.о - t_5,6 = 18 - 6 = 12,

t₄^п^.^о = min { 18 - 5, 12 - 7 } = 5, t₃^п^.^о = min { 18 - 2, 12 - 3 } = 9,

^j^{=5,6
j = 5,6}

t₂^п^.^о = min { 5 - 2, 9 - 3 } = 3, t₁^п^.^о = t₃^п^.^о - t_1,3 = 9 - 2 = 7,

^j^{= 3,4}

t₀^п.о = min { 7 - 2, 3 - 3 } = 0.

^j^{= 1,2}

Вычислим t_ij^п.н - поздний срок начала работы. Он является наиболее поздним (максимальным) из допустимых моментов начала данной работы, при котором еще возможно выполнение всех последующих работ в установленный срок:

t_ij^п.н = t_j^п.о- t_ij.

Результаты расчетов запишем в табл. 2.

Различают два вида резервов времени: полный резерв (r_п) и свободный резерв (r_св).

Полный резерв времени показывает, на сколько может быть увеличена сумма продолжительности всех работ относительно критического пути. Он представляет собой разность между максимальным отрезком времени, в течение которого может быть выполнена операция, и ее продолжительностью (t_ij) и определяется:

r_п= t_ij^п.н - t_i^p^.н.

Результаты расчета помещены в табл. 2.

Свободный резерв времени - максимальное время, на которое можно отстрочить начало или увеличить продолжительность работы при условии, что все события наступают в ранние сроки:

r_св_ij = t_j^p^.н - t_i^р.н - t_ij.

Произведем вычисления свободного резерва для всех работ:

r_св_0,1 = t₁^p^.н - t₀^р.н - t_0,1= 2 - 0 - 2 = 0,

r_св_0,2 = t₂^p^.н - t₀^р.н - t_0,2= 3 - 0 - 3 = 0,

r_св_1,3 = t₃^p^.н - t₁^р.н - t_1,3= 6 - 2 - 2 = 2,

r_св_2,3 = t₃^p^.н - t₂^р.н - t_2,3= 6 - 3 - 3 = 0,

………………………………………..

r_св_5,6 = t₆^p^.н - t₅^р.н - t_5,6= 18 - 12 - 6 = 0.

Результаты расчета критического пути и резервов времени некритических операций представлены в табл. 2. Следует отметить, что критические операции должны иметь нулевой полный резерв времени, при этом свободный резерв также должен быть равен нулю.

Используя результаты вычислений при прямом и обратном проходах, можно определить операции критического пути. Операция (i, j) принадлежит критическому пути, если она удовлетворяет условиям:

t_i^р.н = t_i^п.о,

t_j^р.н = t_j^п.о,

t_j^р.н - t_i^р.н = t_j^п.о - t_i^п.о = t_i_j.

Для рассматриваемого примера критический путь включает операции (0,2), (2,4), (4,5), (5,6) с общим временем выполнения работ 18 недель.

При небольшом числе работ критические операции могут быть найдены перебором возможных путей. Так, для рассматриваемого случая:

путь (0, 2), (2, 4), (4, 6) имеет продолжительность 10 недель;

(0, 2), (2, 3), (3, 5), (5, 6) - 15 недель;

(0, 2), (2, 4), (4, 5), (5, 6) - 18 недель;

(0, 1), (1, 3), (3, 5), (5, 6) - 13 недель;

(0, 1), (1, 3), (3, 6) - 6 недель.

Наибольшим является путь 18 недель, содержащий операции (0, 2), (2, 4), (4, 5), (5, 6), которые являются критическими.

Таблица 2

Работа

(i, j)

Продолжительность

T_ij

Раннее

Позднее

Полный резерв

r_п

Свободный резерв

r_св

начало

t_j^p^.н

окончание

t_ij^p^.^o

начало

t_ij^п.н

окон-чание

t_j^п.о

(0,1)

(0,2)

(1,3)

(2,3)

(2,4)

(3,5)

(4,5)

(3,6)

(4,6)

(5,6)

0 ^К

Примечание: к - критические операции.

Учет стоимостных факторов при реализации сетевого графика

Стоимостные факторы при реализации сетевого графика учитываются путем определения зависимости "затраты - продолжительность" для каждой операции. При этом рассматриваются прямые затраты, а косвенные типа административных или управленческих расходов не принимаются во внимание.

На рис. 7 показана линейная зависимость стоимости операции от ее продолжительности. Точка (D_В,С_В), где D_В - продолжительность операции, а С_В - ее стоимость, соответствует нормальному режиму выполнения операции. Продолжительность операции можно уменьшить (сжать), увеличив интенсивность использования ресурсов, а следовательно, увеличив стоимость операции. Однако существует предел, называемый минимальной продолжительностью операции. За точкой, соответствующей этому пределу (точка максимально интенсивного режима), дальнейшее увеличение интенсивности использования ресурсов ведет лишь к увеличению затрат без сокращения продолжительности операции. Этот предел обозначен на рис. 7 точкой А с координатами (D_А,С_А).

Затраты

Рис. 7

Линейная зависимость "затраты - продолжительность" принимается из соображений удобства, так как ее можно определить для любой операции по двум точкам нормального и максимально интенсивного режимов, т. е. по точкам А и В.

Использование нелинейной зависимости "затраты - продолжительность" существенно усложняет вычисления. Поэтому иногда нелинейную зависимость можно аппроксимировать кусочно-линейной (рис. 8), когда операция разбивается на части, каждая из которых соответствует одному линейному отрезку. Следует отметить, что наклоны этих отрезков при переходе от точки нормального режима к точке максимально интенсивного режима возрастают. Если это условие не выполняется, то аппроксимация не имеет смысла.

Определив зависимость "затраты - продолжительность", для всех операций сети принимают нормальную продолжительность. Далее рассчитывается сумма затрат на все операции сети при этой продолжительности работ. На следующем этапе рассматривается возможность сокращения продолжительности работ. Этого можно достичь за счет уменьшения продолжительности какой-либо критической операции, только критические операции и следует подвергать анализу.

Чтобы добиться сокращения продолжительности выполнения работ при минимально возможных затратах, необходимо в максимально допустимой степени сжать ту критическую операцию, у которой наклон кривой "затраты - продолжительность" наименьший. В результате сжатия критической операции получают новый календарный график, возможно, с новым критическим путем. Стоимость работ при новом календарном графике будет выше стоимости предшествующего графика. На следующем этапе этот новый график вновь подвергается сжатию за счет следующей критической операции с минимальным наклоном кривой "затраты - продолжительность" при условии, что продолжительность этой операции не достигла минимального значения. Подобная процедура повторяется, пока все критические операции не будут находиться в режиме максимальной интенсивности. Полученный таким образом оптимальный календарный график соответствует минимуму прямых затрат.

Затраты

Рис. 8.

Пример. Постройте график работ и, сжимая операции, определите минимально возможный критический путь и стоимость работ до сжатия и после него. Необходимые исходные данные указаны в табл. 3.

Таблица 3

Операция	Нормальный режим		Максимальный режим
Операция	Продолжи-тельность, дн.	Затраты, тыс. р.	Продолжительность, дн.	Затраты, тыс. р.
0,1	30	20	25	30
1,2	60	40	45	60
1,3	50	30	40	40
1,4	30	70	70	100
2,4	90	60	65	70
3,4	80	25	20	25
4,5	20	20	17	25
Итого	360	265	282	350

Решение. Составим график выполнения работ (рис. 8).

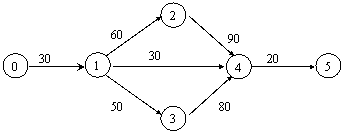
Рис. 8

Перебором работ определим критический путь. По графику путь (0,1), (1,2), (2,4), (4,5) имеет продолжительность 200 дн.; (0,1), (1,3), (3,4), (4,5) - 180 дн.; (0,1), (1,4), (4,5) - 80 дн. Таким образом, критическим путем графика является путь, на котором находятся работы (0,1), (1,2), (2,4), (4,5) продолжительностью

30 дн. + 60 дн. + 90 дн. + 20 дн. = 200 дн.

График выполнения работ может быть сжат за счет достижения на некоторых работах максимально интенсивного режима работы.

Вычислим наклоны кривой "затраты - продолжительность" для каждой операции.

Наклон определяется как частное от деления прироста стоимости на уменьшение времени выполнения работ.

Результаты расчетов приведены в табл. 4.

Таблица 4

Операция

Наклон

0,1

1,2

1,3

2,4

3,4

1,4

4,5

1,3

1,5

0,7

1,7

Учитывая наклоны кривой, производим в первую очередь сжатие операций, имеющих наименьший наклон. Путь (0,1), (1,2), (2,4), (4,5) может быть сжат до 157 дн., путь (0,1), (1,4), (4,5) - до 72 дн., путь (0,1), (1,3), (3,4), (4,5) - до 157 дн. Дальнейшее сжатие путей (0,1), (1,4), (4,5) и (0,1), (1,3), (3,4), (4,5) нецелесообразно, так как стоимостные резервы пути (0,1), (1,2), (2,4), (4,5) исчерпаны полностью. Этот путь является критическим и дальнейшее уменьшение критического пути не представляется возможным. Таким образом, критический путь сокращен с 200 до 157 дн.

Получим сетевой график (рис. 9).

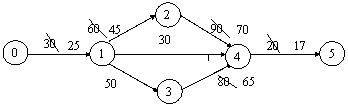
Рис. 9

Новый график имеет два критических пути: (0,1), (1,2), (2,4), (4,5) и (0,1), (1,3), (3,4), (4,5).

Стоимость сжатия работ составит:

(0, 1): 30 тыс. р. - 20 тыс. р. = 10 тыс. р.;

(1, 2): 60 тыс. р. - 40 тыс. р. = 20 тыс. р.;

(2, 4): 100 тыс. р. - 70 тыс. р. = 30 тыс. р.;

(3, 4): 70 тыс. р. - 60 тыс. р. = 10 тыс. р.;

(4, 5): 25 тыс. р. - 20 тыс. р. = 5 тыс. р.;

10 тыс. р. + 20 тыс. р. + 30 тыс. р. + 10 тыс. р. + 5 тыс. р. = 75 тыс. р.

При нормальном режиме работ критический путь составляет 200 дн., стоимость работ - 265 тыс. р.

Критический путь может быть уменьшен до 157 дн., при этом минимальная стоимость работ составляет 265 тыс. р. + 75 тыс. р. =
= 340 тыс. р.