Дерево решений

На практике результат одного решения, как правило, приводит к необходимости принятия следующего решения и т. д.

Графически подобные процессы могут быть представлены с помощью дерева решений. Дерево представляет собой связный граф без циклов, имеющий ствол и ветви, и облегчает описание многоэтапного процесса принятия управленческого решения в целом. Оно дает возможность рассмотреть различные ситуации, соотнести с ними финансовые результаты, скорректировать их в соответствии с приписанной им вероятностью, а затем сравнить альтернативы и выбрать наилучший вариант действий.

Составляя дерево решений, рисуют ствол и ветви, отображающие структуру проблемы. Располагают дерево решений слева направо. Ветви обозначают возможные альтернативные решения, которые могут быть приняты, и возможные исходы, возникающие в результате этих решений.

Квадратные узлы на дереве решений обозначают места, в которых принимаются решения, круглые узлы - места исходов. Так как не представляется возможным влиять на появление исходов, то в круглых узлах вычисляют вероятности их появления. Когда все решения и их исходы указаны на дереве, оценивается каждый из вариантов и проставляются денежные доходы. Все расходы, вызванные решениями, проставляются на соответствующих ветвях. Рассмотрим задачу с применением дерева решений.

Пример 1. Фирма может принять решение о строительстве среднего и малого предприятия. Малое предприятие впоследствии можно расширить. Решение определяется будущим спросом на продукцию, которую предполагается выпускать на сооружаемом предприятии. Строительство среднего предприятия экономически оправдано при высоком спросе. С другой стороны, можно построить малое предприятие и через два года его расширить.

Фирма рассматривает данную задачу на десятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого и низкого уровней спроса равны 0,7 и 0,3, соответственно. Строительство среднего предприятия обойдется в 4 млн. р., малого - в 1 млн. р. Затраты на расширение через два года малого предприятия оцениваются в 3,5 млн. р.

Ожидаемые ежегодные доходы для каждой из возможных альтернатив:

- среднее предприятие при высоком (низком) спросе дает 0,9 (0,2) млн. р.;

- малое предприятие при низком спросе дает 0,1 млн. р.;

- малое предприятие при высоком спросе дает 0,2 млн. р. в течение 10 лет;

- расширенное предприятие при высоком (низком) спросе дает 0,8 (0,1) млн. р.;

- малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает
0,1 млн. р. в год за остальные восемь лет.

Определить оптимальную стратегию фирмы в строительстве предприятий.

Решение. Данная задача является многоэтапной, так как если фирма решит строить малое предприятие, то через два года она может принять решение о его расширении. В этом случае процесс принятия решения состоит из двух этапов: решения в настоящий момент времени о размере предприятия и решения, принимаемого через два года о необходимости его расширения.

Задача представлена в виде дерева решений. Предполагается, что спрос может оказаться высоким и низким. Дерево имеет два типа вершин: "решающие" вершины, обозначенные квадратными узлами, и "случайные" вершины, показанные круглыми узлами.

Р=0,7 0,9 млн. р.

Р=0,3 0,2 млн. р.

Среднее Р=0,7

предприятие Расширение 0,8 млн.р.

4 млн.р Р=0,3 0,1 млн.р.

Годовой 3,5 млн.р.

доход Без Р=0,7 0,2 млн.р.

Малое 0,2 млн.р. Р=0,7 расширения Р=0,3 0,1 млн.р.

предприятие Р=0,3 0,1 млн.р.

1 млн.р.

1 этап (2 года) 2 этап (8 лет)

Рис. 6.2

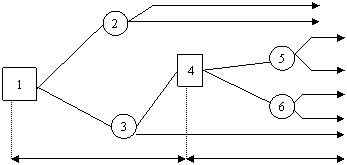
Начиная с вершины 1, являющейся "решающей", необходимо принять решение относительно размера предприятия. Вершины 2 и 3 являются "случайными". Фирма будет рассматривать возможность расширения малого предприятия только в том случае, если спрос по истечении первых двух лет установится на высоком уровне. Поэтому в вершине 4 принимается решение о расширении или нерасширении предприятия. Вершины 5 и 6 будут "случайные".

Произведем расчеты для каждой из альтернатив. Вычисления начнем со 2 этапа. Для последних восьми лет альтернативы, относящиеся к вершине 4, оцениваются:

ДР = (0,8 × 0,7 + 0,1 × 0,3) × 8 - 3,5 = 1,22 млн. р.;

ДБР = (0,2 × 0,7 + 0,1 × 0,3) × 8 = 1,36 млн. р.,

где ДР - доход с расширением;

ДБР - доход без расширения предприятия.

Таким образом, в вершине 4 выгоднее не проводить расширение, при этом доход составит 1,36 млн. р.

Теперь для дальнейших расчетов оставим одну "ветвь", выходящую из вершины 4, которой соответствует доход 1,36 млн. р. за остальные восемь лет (рис. 6.2). Перейдем к вычислениям 1 этапа. Для вершины 1:

ДС = (0,9 × 0,7 + 0,2 × 0,3) × 10 - 4,0 = 2,9 млн. р.;

ДМ = 1,36 + 0,2 × 0,7 × 2 + 0,1 × 0,3 × 10 - 1,0 = 0,94 млн. р.,

где ДС - доход среднего;

ДМ - доход малого предприятия.

Сравнивая полученные в вершине 1 доходы среднего и малого предприятий, видим, что более предпочтительным является вариант строительства среднего предприятия. Таким образом, фирме целесообразно построить среднее предприятие. Оценим степень риска каждого решения по величине среднеквадратического отклонения:

s₁ = = 2,23 млн. р.;

s₂ = = 0,65 млн. р.

Рассматривая среднеквадратические отклонения, следует отметить, что решение по строительству малого предприятия дает более гарантированный доход.