Построение минимального

остовного дерева сети

 

В экономических приложениях графы принято называть сетями, а их вершины - узлами. Каждому ребру (дуге) придают некоторое числовое значение, которое в зависимости от смысла задачи может обозначать расстояние, пропускную способность, время и т.д. С каждым видом сети связан определенный тип потоков (например, поток нефти в нефтепроводах, автомобильные потоки в сети городских дорог).

Определение 1. Остовным деревом сети называется дерево, содержащее все узлы сети.

Пример 1. Рассмотрим сеть с пятью узлами:

 

 

 

 

 

 


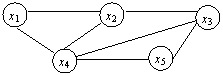
Для данной сети можно построить следующие остовные деревья:

 

 

 

 


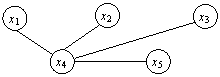
a)

 

 

 

 

 

 


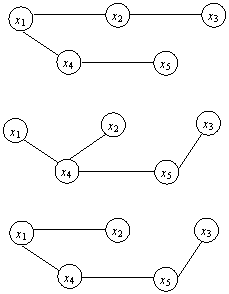
b)

 

 

 

 

 

c)

 

 

 

 

 

d)

 

 

и т.д. Можно утверждать, что для данной сети существует множество остовных деревьев.

При изучении сетей возникает задача построения минимального остовного дерева, т.е. задача соединения всех узлов сети с помощью путей наименьшей длины. Примером такой задачи является проектирование сети дорог, соединяющих населенные пункты, где дороги, соединяющие два пункта, могут проходить через другие населенные пункты. Наиболее экономичный проект должен минимизировать общую длину дорог.

Рассмотрим процедуру построения минимального остовного дерева. Обозначим:

X={ x1, x2, …, xn } - множество узлов сети;

Ck - связное множество узлов сети, соединенных алгоритмом после выполнения k-й итерации.

 - множество узлов сети, не соединенных с узлами множества Ck после выполнения k-й итерации.

Алгоритм построения минимального остовного дерева сети

1.     Выбрать произвольный узел сети xi, C1={xi}, = X\{xi}.

2.     Выбрать из оставшихся узлов узел xj, ближайший к множеству узлов C1, C2={ xi, xj }, = X\{ xi, xj }.

3.     Выбрать из множества  узел, ближайший к узлам множества C2 , включить его в множество C2 и исключить из множества .

За конечное число шагов будут обработаны все узлы сети и построено минимальное остовное дерево. Cn=X, =f.

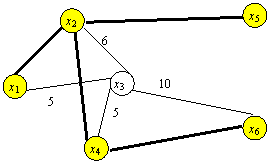
Пример 2. Телевизионная компания планирует подключение к кабельной сети пяти новых районов. Структура планируемой сети и расстояния  между пунктами заданы рисунком.

 

 

 

 

 

 

 

 

 

 


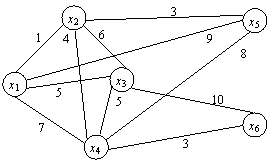
Требуется спланировать наиболее экономичную кабельную сеть.

Проведем пошаговое построение минимального остовного дерева для данной сети. C0=f, =X={ x1, x2, x3, x4, x5, x6 }. Начнем с узла x1.

 

 

 

 

 

 

 

 

 

 


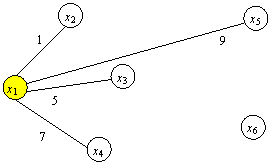
Итерация 1. C1={ x1 }, ={ x2, x3, x4, x5, x6 }, min (1,5,7,9)=1. Ближайшим узлом к множеству C1 является x2. Добавляем его к остовному дереву с ребром длиной 1 км.

 

 

 

 

 

 

 

 

 

 

 

 


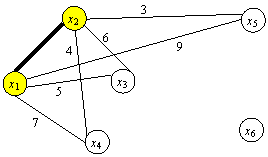
Итерация 2. C2={x1, x2}, ={x3, x4, x5, x6}, min (3,4,5,6,7,9)=3. Ближайшим узлом к множеству C2 является x5. Добавляем его к остовному дереву с ребром длиной 3 км.

 

 

 

 

 

 

 

 

 

 

 


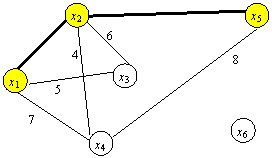
Итерация 3. C3={x1, x2, x5}, ={x3, x4, x6}, min (4,5,6,7,8)=4. Ближайшим узлом к множеству C3 является x4. Добавляем его к остовному дереву с ребром длиной 4 км.

 

 

 

 

 

 

 

 

 

 

 


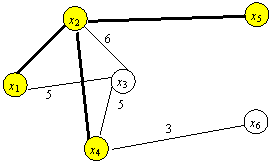
Итерация 4. C4={x1, x2, x4, x5}, ={x3, x6}, min (3,5,6)=3. Ближайшим узлом к множеству C4 является x6. Добавляем его к остовному дереву с ребром длиной 3 км.

 

 

 

 

 

 

 

 

 

 


Итерация 5. C5={x1, x2, x4, x5, x6}, ={ x3 }, min (5,6,10)=5. Ближайшим узлом к множеству C5 является x3. Добавляем его к остовному дереву с ребром длиной 5 км. При этом возможно два альтернативных соединения ( x1, x3 ) и ( x4, x3 ) длиной 5 км.

 

 

 

 

 

 

 

 

 

 


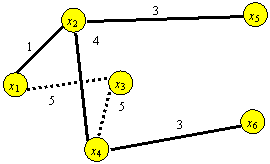
Процесс построения минимального остовного дерева завершен.

C6=X={x1, x2, x3, x4, x5, x6}, =f. Минимальная длина телевизионного кабеля составит 1+3+4+5+3=16 км.