Связность графа, деревья

Определение 1. Две вершины графа называются связными, если в графе существует путь с концами в этих вершинах, и несвязными в противном случае.

Определение 2. Граф называется связным, если любые две его вершины связны, и несвязным в противном случае.

Пример 1. Существует ли компания из шести человек, в которой каждый знаком с двумя, и только с двумя другими? Вариантов таких компаний может быть два.

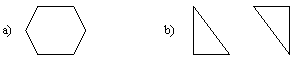
В первом случае мы имеем связный граф, во втором - несвязный.

Теорема 1. Связный граф G(X,T) представляет собой простой цикл тогда, и только тогда, когда каждая его вершина имеет степень 2.

Доказательство.

Необходимость. Пусть граф G(X,T) представляет собой простой цикл. Он является замкнутым простым путем. Из любой его вершины можно попасть в любую другую, не проходя ни через какую вершину два раза. Очевидно, что степень любой вершины такого графа равна 2.

Достаточность. Пусть граф G(X,T) связный и степень каждой его вершины равна 2. Любые две его вершины соединены путем. Возьмем произвольную вершину. Пойдем по одному из двух ребер, к которым принадлежит эта вершина. Мы попадем в следующую вершину, из которой выходит два ребра. По одному мы пришли. Двигаемся далее по второму ребру. Таким образом, все вершины графа будут пройдены и мы вернемся в исходную вершину. Путь замкнется. Следовательно, этот граф является циклом.

Определение 3. Ребро (x_i, x_j) называется мостом, если в графе G(X,T), полученном после удаления ребра (x_i, x_j), вершины x_i и x_j несвязны.

Пример 2.

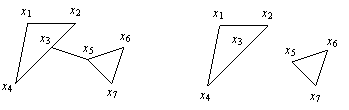
В исходном графе ребро (x₃, x₅) является мостом.

Существует несколько признаков мостов:

1) Ребро (x_i, x_j) является мостом тогда, и только тогда, когда (x_i, x_j) является единственным путем, соединяющим вершины x_i и x_j.

2) Ребро (x_i, x_j) является мостом тогда, и только тогда, когда найдутся две вершины x_k и x_m, такие, что любой путь, соединяющий их, содержит вершины x_i и x_j.

3) Ребро (x_i, x_j) является мостом тогда, и только тогда, когда оно не принадлежит ни одному циклу.

Определение 4. Связный граф без циклов называется деревом.

Определение 5. Вершина дерева, имеющая степень 1, называется висячей.

По аналогии с генеалогическими деревьями вводятся родовые понятия для вершин.

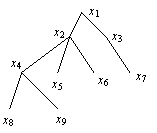Пример 3.

Вершина x₁ называется корневой, пути от нее называются ветвями. Вершина x₂ называется родительской по отношению к вершинам x₄, x₅, x₆ и прародительской по отношению к вершинам x₈, x₉. Вершины x₂ и x₃ называются дочерними к вершине x₁.

Пример 4. Кубок по настольному теннису разыгрывают 16 команд по олимпийской системе. Схему турнира можно изобразить деревом.

Любое ребро в дереве является мостом. Для каждой пары вершин дерева существует единственный соединяющий их путь.

Теорема 2. Дерево с n вершинами имеет n-1 ребро.