Теоремы об экстремуме целевой функции

Теорема 1. Если область допустимых решений (ОДР) системы ограничений ЗЛП ограниченна, то оптимальное решение существует и совпадает хотя бы с одним из опорных решений.

Доказательство. Так как целевая функция ЗЛП непрерывна, а ОДР ограниченна, то по свойству непрерывной функции, заданной в ограниченной области (теорема Вейерштрасса), следует, что она в этой области достигает своего наибольшего и наименьшего значения, т.е. оптимальное решение существует.

Докажем, что оптимальное решение совпадает хотя бы с одним из опорных решений. Предположим противное, оптимальное решение не является опорным: . Пусть - опорные решения ОДР. Тогда можно представить как выпуклую линейную комбинацию опорных решений, т.е.

, где и , .

Пусть задача решается на max, т.е. max.

Найдем , для этого целевую функцию запишем в виде скалярного произведения двух факторов и ,

.

Тогда

.

Выберем из всех значений наибольшее: и заменим все значения наибольшим, сумма при этом может только увеличиться, так как все .

Тогда

.

Получим противоречие , следовательно оптимальное решение совпадает хотя бы с одним из опорных решений.

Теорема 2. Если область допустимых решений системы ограничений ЗЛП неограниченна, то оптимальное решение существует и совпадает хотя бы с одним из опорных решений, если целевая функция ограничена сверху для задачи на максимум и снизу для задачи на минимум.

Определение. Случай, когда оптимальное решение ЗЛП совпадает с несколькими опорными решениями, называется случаем альтернативного оптимума.

Теорема 3. Если оптимальное решение совпадает с несколькими опорными решениями, то любая выпуклая линейная комбинация этих оптимальных решений является также оптимальным решением задачи.

Доказательство. Пусть задача имеет k оптимальных решений: т.е.

max.

Составим выпуклую линейную комбинацию этих оптимальных решений:

, где , и .

Покажем, что также оптимальное решение, для этого найдем значение целевой функции от :

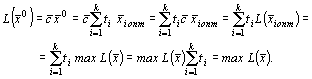
То есть - оптимальное решение.

Если задача имела два оптимальных решения и , то любая точка отрезка является также оптимальным решением, т.е.

, где 0 £ t £ 1.

Вывод. Из теорем следует, что оптимальное решение ЗЛП следует искать только среди опорных решений системы ограничений, а так как опорные решения соответствуют угловым точкам ОДР, то оптимальные решения нужно искать среди угловых точек ОДР.