Переход от одной формы ЗЛП к другой

Переход от неканонической формы ЗЛП к канонической.

Теорема 1. Каждому решению неравенства соответствует единственное решение уравнения и неравенства , и наоборот.

Из теоремы следует, что неравенство можно заменить уравнением и неравенством .

Переменную называют балансовой переменной.

Следовательно, чтобы привести задачу к каноническому виду, нужно заменить каждое неравенство системы ограничений соответствующим уравнением и неравенством , введя в каждое неравенство балансовую переменную с коэффициентом +1, если знак неравенства £, и с коэффициентом -1, если знак неравенства ³. В целевую функцию балансовые переменные вводятся с нулевыми коэффициентами.

Если на переменную не наложено условие на неотрицательность, то эту переменную надо представить в виде разности двух неотрицательных переменных: , где

Переход от канонической формы ЗЛП к симметричной форме.

Чтобы перейти от канонической формы ЗЛП к симметричной, нужно найти общее решение системы уравнений:

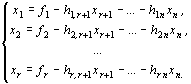
Так как все переменные должны быть неотрицательными, в том числе и базисные, получим систему неравенств:

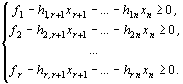
Чтобы исключить базисные переменные из целевой функции, необходимо в целевую функцию вместо базисных переменных подставить их выражения через свободные переменные.

Пример 1. Дана ЗЛП: найти наибольшее значение функции при ограничениях:

.

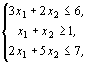
Приведем ее к каноническому виду.

Канонический вид задачи: найти наибольшее значение функции при ограничениях:

.

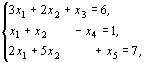
Пример 2. Перейти от канонического вида задачи к симметричному. Найти наибольшее значение функции при ограничениях:

.

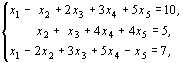
Разрешим систему относительно произвольного базиса, система примет вид

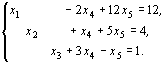
И так как , отбросив базисные переменные, получим систему неравенств

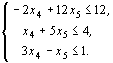
Выразим целевую функцию через свободные переменные:

Симметричный вид задачи: найти наибольшее значение функции при ограничениях:

.