Численные методы поиска стационарных

точек: метод Ньютона и градиентные методы

Метод Ньютона

Экстремум функции следует искать в стационарной точке, которая является решением системы уравнений:

_,(1)

где

Решить систему (1) в некоторых случаях бывает довольно сложно. Особенно, если это система нелинейных уравнений. В таких случаях применяют численные методы. В частности, метод последовательных приближений.

Начнем с функции одной переменной. Рассмотрим уравнение где - нелинейная функция скалярного аргумента. Предположим, что найти точное значение корней не удается. Найдем приближенное значение его корней.

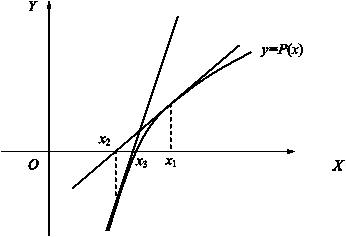
Предположим, что известен интервал, содержащий один корень уравнения. Начнем с произвольной точки х₁ из этого интервала. Построим в этой точке касательную к функции . Как известно, уравнение касательной в точке с угловым коэффициентом записывается так:

или

Найдем точку очередного приближения. Это будет точка х₂, в которой касательная пересекает ось ординат. Сделаем это из условия

Отсюда получается, что

Теперь строим касательную в точке (х₂ Р(х₂)) и далее аналогичным образом находим точку х₃.В результате получаем последовательность точек х₁, х₂, х₃, …, х_k, х_k₊₁, где каждое последующее значение находится через предыдущее по формуле

. (2)

Учитывая, что , соотношение (2) можно переписать в виде

. (3)

Формулу (3) можно распространить на общий случай, когда вместо скалярной величины в качестве аргумента функции имеем вектор :

, (4)

где

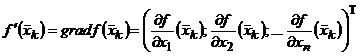- градиент,

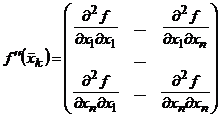- матрица Гессе.

Итерационный процесс продолжается до тех пор, пока не будет обнаружено, что произошло достаточное приближение к искомой точке. Критерием этого является выполнение условия , где - длина градиента, - достаточно малое положительное число.

В некоторых случаях процесс сходится к искомой точке за конечное число шагов. Например, для квадратичной функции метод дает результат, за число шагов не превышающих n.

Пример. Найти стационарную точку функции

Решение. Решим задачу классическим способом, затем проиллюстрируем метод Ньютона.

1) Решение классическим способом:

- стационарная точка.

2) Решим задачу методом Ньютона. В данном случае формулу (4) можно записать так:

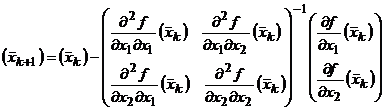Найдем градиент и матрицу Гессе для заданной функции:

, .

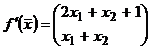Предположим, что исходная точка , тогда

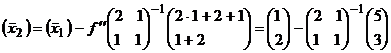Вычислим обратную матрицу к матрице Гессе:

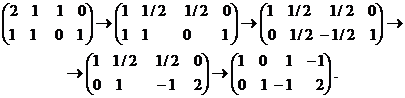
Таким образом,

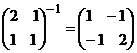Тогда координаты очередной точки

Точка следующего приближения

Как видим, получена точка, совпадающая с той, которая была на предыдущем шаге, следовательно, стационарная точка найдена. Заметим, что это решение совпадает с тем, которое было найдено классическим способом.

Градиентный метод

Известно, что градиент скалярной функции в некоторой точке направлен в сторону наискорейшего возрастания функции и ортогонален линии уровня в этой точке. Находясь в очередной точке и каждый раз выбирая в качестве направления движения градиент (или антиградиент - вектор противоположной направленности), мы приходим к итерационному процессу возрастания (убывания) функции. Этот итерационный процесс можно выразить следующей формулой:

где - параметр, определяющий длину и направление очередного шага;

- градиент функции в текущей точке.

Существует несколько вариантов градиентного метода в зависимости от того, как на каждой итерации осуществляется выбор параметра . Рассмотрим эти варианты.

1. Градиентный метод с постоянным параметром шага предполагает, что = , где - постоянная величина, например
= 1. Тогда шаг будет равен длине градиента в текущей точке и направлен в сторону возрастания функции. По мере приближения к стационарной точке (если функция вообще имеет стационарную точку локального максимума) длина шага будет уменьшаться и процесс приближения будет замедляться.

2. Градиентный метод с дроблением шага. Параметр на каждой итерации вычисляется по формуле

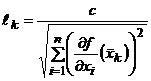в результате чего длина шага не зависит от длины градиента и остается постоянной, равной . Кроме того, выбирая знак параметра , можно выбирать направление движения - к максимуму () или к минимуму (). Однако может случиться так: приблизившись к стационарной точке, мы сделаем очередной шаг, который окажется слишком большим. Обнаружится, что (предполагается, что мы ищем максимум), т.е. полученный результат хуже предыдущего. Это значит, что мы вошли в область стационарной точки, необходимо уменьшить шаг. В соответствии с этим параметр уменьшается, например, в 2 раза. И процесс продолжается. Так будет происходить до тех пор, пока длина шага не станет достаточно малой. Этот метод прост, но его существенный недостаток состоит в том, что выбор параметра приходится делать субъективно.

3. Градиентный метод наискорейшего подъема (спуска). Здесь длина шага берется не произвольно, а так, что на каждой итерации достигается максимальное увеличение целевой функции. То есть длина шага выбирается оптимальным образом, путем решения вспомогательной задачи.

Беря производную по и приравнивая полученное выражение к нулю, мы получаем:

Это выражение показывает, что направления движения на двух последних шагах ортогональны.

Все три рассмотренных варианта метода имеют общий недостаток, который состоит о том, что они плохо работают, если поверхность функции напоминает "овраг" или "гребень". В этом случае сходимость даже в случае применения наискорейшего подъема (спуска) сильно замедляется. Существуют более эффективные варианты градиентного метода, способные преодолевать это обстоятельство, но их рассмотрение выходит за рамки нашего учебника.