Модель олигополии Курно

Базовая модель дуополии Курно может быть распространена и на отрасль с произвольным количеством субъектов.

Пусть на рынке конкурируют п продавцов с объемами выпуска продукции q₁, q₂,…,q_n и равными издержками производства

TC_i =cq_i.

Суммарный объем продаж на рынке известен и задан функцией спроса

Р=P(),

где

.

В частности, предполагается, что рыночный спрос задан убывающей линейной функцией вида

, где

или

.

Прибыль каждого участника олигополии зависит от структуры предложения всех участников рынка:

П_i=П_i (q₁, q₂,…,q_n).

С точки зрения i-го олигополиста, стремящегося максимизировать свою прибыль за счет оптимального выбора уровня производства, прибыль выражается функцией

Условием максимизации функции прибыли будет равенство нулю производной

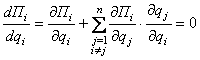. (1)

Присутствующие в последнем равенстве выражения называют коэффициентами предполагаемых вариаций. Они показывают, как изменится объем выпуска каждого из конкурентов при изменении объема выпуска i-го соперника на единицу. Как правило, эти коэффициенты неизвестны, но можно использовать их ожидаемые (гипотетические) значения.

Из условия (1) можно получить зависимость объема предложения каждого олигополиста от объемов предложений конкурентов

,

Это уравнение задает кривую реагирования (линию реакции) i-го олигополиста.

Модель Курно строится в предположении, что уровень выпуска фирмы не зависит от уровней выпуска конкурентов, а соответственно, предполагаемые вариации принимаются равными нулю.

Прибыль в данном случае выражается разностью между выручкой и издержками:

П_i = ТR_i − TC_i = Pq_i − cq_{i ,}

.

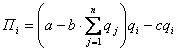Тогда условие (1) принимает вид:

, (2)

При условия (2) задают систему уравнений. Решение системы позволяет найти точку равновесия.

Решение задачи нахождения оптимальных параметров рыночного взаимодействия можно упростить, если принять во внимание принятое в модели наличие равных условий для всех конкурентов. Очевидно, что равновесные объемы предприятий одинаковы. Тогда вместо каждой из переменных можно использовать одну переменную q, в результате чего получим:

.

Отсюда определим равновесный выпуск:

.

При таком объеме выпуска каждого олигополиста общий выпуск отрасли составит

,

и при равновесной цене

каждый получит оптимальную прибыль

.

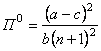Приведенные формулы для расчета параметров рыночного равновесия обобщают рассмотренные выше случаи: при п=1 получаеются монопольные значения объема, цены и прибыли; при п=2 модель сводится к дуополии Курно. Заметим, что при дуополии отраслевой выпуск больше, чем при монополии; а для равновесной цены динамика обратная: при дуополии она ниже, чем при монополии. Анализ изменения параметров олигополии Курно приводит к выводу о том, что с увеличением числа конкурентов суммарный объем продукции растет, а выпуск каждого олигополиста падает. При наблюдаемом понижении равновесной цены это приводит к уменьшению прибыли.

При достаточно большом числе фирм-производителей () равновесная цена приближается к величине предельных издержек, выпуск каждой фирмы становится мал по сравнению с суммарным выпуском, и рынок олигополии Курно превращается в рынок совершенной конкуренции.