Модель дуополии Курно.

Модель Курно является одной из основных моделей некооперированной количественной олигополии. Она имеет важное методологическое значение, т.к. позволяет не только проанализировать различные возможности стратегического взаимодействия участников рынка, но и понять основные проблемы применения моделей.

Пусть на рынке конкурируют две фирмы, производящие однородную продукцию и самостоятельно (без сговора) принимающие решение относительно объема ее выпуска. В классической модели Курно каждый дуополист предполагает, что объем выпуска соперника постоянен и не зависит от изменения его собственного объема выпуска.

Предполагается, что рыночный спрос известен и задается убывающей линейной функцией, выражающей зависимость рыночной цены Р от количества продукции Q:

,

(где , а объем предложения Q равен сумме объемов предложения первой и второй фирм:

Q₁= q₁ + q₂

Таким образом,

.P=a-b(q₁ + q₂)

Предположим также, что обе фирмы имеют равные издержки производства:

ТС₁ = ТС₂ = сq₁ = cq₂.

Определим условия равновесия – такого состояния рынка, при котором прибыли обеих фирм максимально возможны.

Прибыль каждой из фирм равна разности между выручкой и издержками:

П₁= ТR₁ − TC₁ = Pq₁ − cq_{1 ,}

П₁= (a − bq₁ − bq₂) q₁ − cq₁,

П₂= ТR₂ − TC₂ = Pq₂ − cq_{2 ,}

П₂= (a − bq₁ − bq₂) q₂ − cq_2.

Линии уровня функции прибыли называют изопрофитами. Они представляют собой совокупность точек, в каждой из которых величина прибыли одного из олигополистов одинакова.

Необходимое условие экстремума функции прибыли имеет вид:

,

.

Отсюда найдем уравнения, выражающие оптимальный уровень выпуска продукции дуополиста через оптимум выпуска его конкурента:

(*)

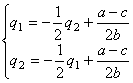Линии, заданные уравнениями (*) называют линиями реакции дуополистов Курно. (Линии реакции иначе называют кривыми реагирования или кривыми наилучшего ответа). В каждой точке линии реакции значение прибыли i-го олигополиста максимально для соответствующего объема выпуска конкурента. Точка равновесия, если она существует, является точкой пересечения линий реакций всех участников рынка.

В точке равновесия оба равенства (*) должны выполняться одновременно. Найдем ее координаты, решив соответствующую систему уравнений:

.

Линии реакции дуополистов, заданные уравнениями (*), изображены прямыми (1) и (2):

q₁

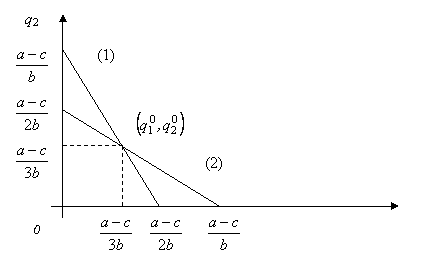
Заметим, что достаточное условие экстремума (отрицательные вторые производные) подтверждает наличие максимума прибыли дуополистов в точке равновесия:

.

Полученные равновесные значения объемов выпуска желательны для обеих фирм, т.к. обеспечивают каждому дуополисту оптимальную прибыль в размере

при равновесной цене .

Представляет интерес графическая интерпретация модели. Функция прибыли первого дуополиста является функцией двух переменных

= (a−bq₁−bq₂)q₁−cq₁.

Ее линии уровня – изопрофиты – задаются уравнениями вида ,

где К – произвольная постоянная.

Имеем:

(a−bq₁−bq₂)q₁−cq₁=К,

.

Для исследования формы кривой найдем производные q₂ по q₁:

.

Нетрудно видеть, что в положительной полуплоскости изопрофита является выпуклой вверх кривой, имеющей одну точку максимума

.

Рост параметра К характеризуется смещением точки максимума вправо и убыванием значения максимума, т.е. «верхушка» кривой с увеличением К скользит вправо вниз. Следовательно, чем ближе к оси q₁ расположена изопрофита, тем более высокому уровню прибыли она соответствует.

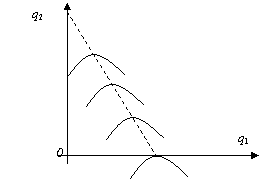
Рассмотрим ситуацию с точки зрения условно первого дуополиста. Зафиксируем некоторый объем выпуска конкурента . Соответствующую горизонтальную прямую пересекает бесконечное семейство изопрофит прибыли первого дуополиста. Наиболее выгодный при данных условиях объем выпуска будут задавать абсциссы точек изопрофиты, расположенной ниже других, но проходящей через прямую . Таким образом, наилучшим ответом дуополиста на выбранный уровень выпуска конкурента будет уровень выпуска такой, что точка является точкой касания прямой и некоторой изопрофиты. Совокупность таких точек касания, (соответствующих всевозможным значениям ) образует линию реакции первого дуополиста.

Наибольшую возможную прибыль первый дуополист получит при нулевом объеме выпуска конкурента, когда вершина соответствующей изопрофиты лежит на горизонтальной оси.

При монопольный объем выпуска первой фирмы будет

,

и при монопольной цене

величина ее прибыли будет равна

.

Заметим, что равновесный объем выпуска в дуополии Курно равен 2/3 монопольного равновесного объема - объема, который обеспечил бы фирме максимальную прибыль при условии ухода с рынка конкурента, а равновесная прибыль фирмы составляет 4/9 монопольной равновесной прибыли.