СИСТЕМЫ
МАССОВОГО ОБСЛУЖИВАНИЯ
Системы массового обслуживания (СМО) с отказами
В системах с отказами
заявка, поступившая в момент, когда все каналы обслуживания заняты, немедленно
получает отказ, покидает систему и в дальнейшем процессе обслуживания не
участвует. Имеется n
каналов обслуживания, на которые поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ (величина,
обратная среднему времени обслуживания t![]() ).
).
Вероятность простоя каналов обслуживания
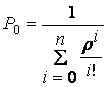 .
.
Требование, поступающее в систему, получает
отказ в том случае, когда все узлы обслуживания заняты. Вероятность отказа исчисляется
по формуле
Р![]() =
=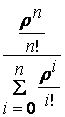 =
= 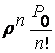 .
.
Относительная пропускная способность, т.е.
вероятность того, что заявка будет обслужена, исчисляется по формуле
P![]() =1-P
=1-P![]() =1-
=1-![]() .
.
Абсолютная пропускная способность, т.е.
среднее число заявок, обслуживаемых в единицу времени, составляет
A=λ
Р![]() .
.
Среднее число занятых каналов
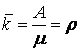 Pобсл.
Pобсл.
Доля каналов, занятых обслуживанием,
составляет
q=![]() .
.
СМО с неограниченным ожиданием
В СМО с неограниченным ожиданием заявка, нашедшая
все каналы занятыми, становится в очередь, на которую не наложено ограничений
ни по длине очереди, ни по времени ожидания. В силу неограниченности очереди
каждая заявка рано или поздно будет обслужена, поэтому Р![]() =1, Р
=1, Р![]() =0. Для СМО с неограниченной очередью накладывается
ограничение
=0. Для СМО с неограниченной очередью накладывается
ограничение ![]() <1. Если это условие нарушено, то очередь растет до
бесконечности, наступает явление «взрыва».
<1. Если это условие нарушено, то очередь растет до
бесконечности, наступает явление «взрыва».
1. Вероятность простоя каналов:
Р![]() =
=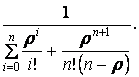
2. Вероятность занятости обслуживанием k каналов:
Pk=![]() , 1
, 1![]() .
.
3. Вероятность занятости обслуживанием всех
каналов при отсутствии очереди:
P![]() =
=![]() .
.
4. Вероятность наличия очереди есть
вероятность того, что число требований в системе больше числа каналов:
P![]() =
=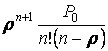 .
.
5. Вероятность для заявки попасть в
очередь есть вероятность занятости всех каналов, эта вероятность равна сумме
вероятностей наличия очереди и занятости всех n каналов при отсутствии очереди:
Pзан =Pп+Pоч =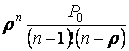 .
.
6. Среднее число занятых обслуживанием
каналов:
![]() =
=![]() =ρ.
=ρ.
7. Доля каналов, занятых обслуживанием:
q=![]() .
.
8. Среднее число заявок в очереди (длина
очереди):
L= .
.
9. Среднее число заявок в системе:
М=L+![]() =L+ρ.
=L+ρ.
10. Среднее время ожидания заявки в очереди:
t=![]() .
.
11. Среднее время пребывания заявки в
системе:
T=t+![]() , T=
, T=![]() .
.
СМО с ожиданием и ограниченной очередью
В системах с ожиданием количество заявок,
стоящих в очереди, ограничено числом m, т.е. заявка, заставшая все каналы
занятыми, становится в очередь, только если в ней находится менее m
заявок. Если число заявок в очереди равно m,
то последняя прибывшая заявка в очередь не становится и покидает систему
не обслуженной.
Системы
с ограниченной очередью являются обобщением двух рассмотренных ранее
СМО: при m=0 получаем СМО с
отказами, при m=![]() CМО с ожиданием.
CМО с ожиданием.
Вероятность простоя каналов обслуживания
Р0=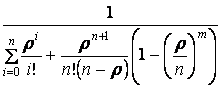 .
.
Вероятность отказа в обслуживании равна
вероятности Рn+m
того, что в очереди уже стоят m заявок:
Ротк=Рn+m=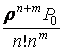 .
.
Относительная пропускная способность есть
величина, дополняющая вероятность отказа до 1, т.е. вероятность обслуживания
Робсл=1-Ротк.
Абсолютная пропускная способность определяется
равенством
А=λ (1-Pотк)=λ Робсл.
Среднее число занятых каналов
![]() =
=![]() =ρРобсл .
=ρРобсл .
Средняя длина очереди, т.е. среднее число
заявок в очереди
L= .
.
Среднее время ожидания обслуживания в очереди
t=![]() .
.
Среднее число заявок в СМО
М=L+![]() .
.
Среднее время
пребывания заявки в СМО
T=t+![]() , T=
, T=![]() .
.
Замкнутые СМО
В замкнутой СМО
циркулирует одно и то же конечное число потенциальных требований. Пока
потенциальное требование не реализовалось
в качестве требования на обслуживание, считается, что оно находится в блоке
задержки. В момент реализации требование поступает в саму систему. Пусть n - число
каналов обслуживания, s - число потенциальных
заявок, n<s, λ -
интенсивность потока заявок каждого потенциального требования, μ -интенсивность
обслуживания,
ρ=![]() .
.
Вероятность простоя системы определяется
формулой
Р0=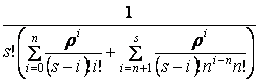 .
.
Финальные вероятности состояний системы
Pk=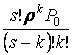 при k<n, Pk=
при k<n, Pk=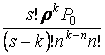 при
при ![]() .
.
Среднее число занятых каналов:
![]() =P1+2P2+…+n(Pn+Pn+1+…+Ps)
=P1+2P2+…+n(Pn+Pn+1+…+Ps)
или
![]() =P1+2P2+…+(n-1)Pn-1+n(1-P0-P1-…-Pn-1).
=P1+2P2+…+(n-1)Pn-1+n(1-P0-P1-…-Pn-1).
Абсолютная пропускная способность системы:
A=![]()
![]() .
.
Среднее число заявок в системе
М=s -![]() =s -
=s -![]() .
.