ДИНАМИЧЕСКОЕ
ПРОГРАММИРОВАНИЕ
Пример 1. Определить оптимальный
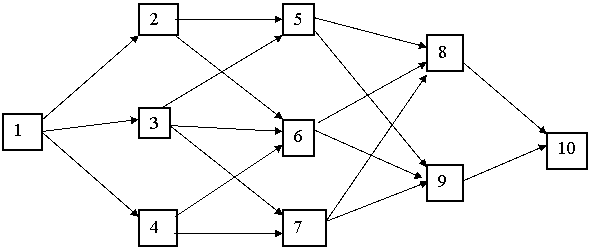
маршрут из пункта 1 в пункт 10 по схеме маршрутов движения (рис. 1).
 9 7
9 7
3 11 5
5
1
7 10 3
4
2 7
7 4
15
13 1
Рис. 1
Каждый квадрат на схеме
изображает один из населенных пунктов, которые для удобства пронумерованы. Стоимость
переезда из пункта i в пункт j
обозначим через сij (значения этих величин для
рассматриваемого примера отмечены на схеме).
Требуется определить такой
путь из пункта 1 в пункт 10, общая стоимость которого является минимальной.
Решение. Используем формулу рекуррентных
соотношений Беллмана:
![]()
где N
- количество
этапов в решении;
![]() - стоимость,
отвечающая стратегии минимальных затрат для пути от пункта i, если до конечного пункта
остается n шагов;
- стоимость,
отвечающая стратегии минимальных затрат для пути от пункта i, если до конечного пункта
остается n шагов;
![]() - решение, позволяющее
достичь
- решение, позволяющее
достичь ![]() .
.
Начинаем поиск оптимального
маршрута от конечного пункта, положив
n=1.
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
n=2.
![]() ;
;
![]() ;
;
![]() .
.
n=3.
![]() ;
;
![]() ;
;
![]() .
.
n=4.
![]() .
.
Таким образом, определен
оптимальный путь:
1-2-6-8-10, затраты по которому составляют ![]() .
.
Пример 2. Решить задачу управления запасами при следующих
условиях: количество отрезков планового периода ![]() , спрос одинаков для всех отрезков
, спрос одинаков для всех отрезков ![]() . Затраты равны
. Затраты равны
![]() , где
, где
![]() - объем производства;
- объем производства; ![]() - запасы на конец отрезка планирования,
- запасы на конец отрезка планирования, ![]() - затраты на хранение
единицы продукции,
- затраты на хранение
единицы продукции, ![]() .
.
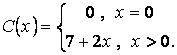
Считаем, что ![]() и
и ![]() - целые, причем
- целые, причем ![]() .
.
Решение.
Используем рекуррентные соотношения:
![]() ,
,
где ![]() - количество этапов в решении;
- количество этапов в решении;
![]() - множество значений переменной
- множество значений переменной ![]() ;
;
![]() - затраты, соответствующие оптимальной стратегии, если до
конца планируемого периода остается
- затраты, соответствующие оптимальной стратегии, если до
конца планируемого периода остается ![]() этапов;
этапов;
![]() - объем производства, обеспечивающий оптимальную стратегию.
- объем производства, обеспечивающий оптимальную стратегию.
Начинаем формирование оптимального плана от последнего
этапа, положив ![]() .
.
Так как ![]() по условию задачи, то
на этом этапе получаем следующие возможные значения функции
по условию задачи, то
на этом этапе получаем следующие возможные значения функции ![]() :
:
![]()
![]()
![]()
![]()
Для удобства занесем эти
данные в таблицу:
|
|
|
|
|
|
0 1 2 3 |
3 2 1 0 |
13 12 11 3 |
3 2 1 0 |
Положим ![]() .
.
Тогда для ![]()
![]() , следовательно
, следовательно
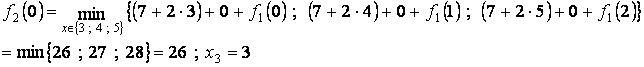 Аналогично
Аналогично
![]()
![]()
![]()
![]()
Таблица имеет вид:
|
|
|
|
|
|
0 1 2 3 4 |
3 ; 4 ; 5 2 ; 3 ; 4 ; 5 1 ; 2 ; 3 ; 4 0 ; 1 ; 2 ; 3 0 ; 1 ; 2 |
26 21 20 16 16 |
3 5 4 0 0 |
Положив ![]() , получим следующую таблицу:
, получим следующую таблицу:
|
|
|
|
|
|
0 1 2 |
3 ; 4 ; 5 2 ; 3 ; 4 ; 5 1 ; 2 ; 3 ; 4 ; 5 |
36 34 33 |
4 5 4 |
Наконец, для
![]() таблица
примет вид:
таблица
примет вид:
|
|
|
|
|
|
0 |
3 ; 4 ; 5 |
49 |
3 ; 4 |
Таким образом, получим два варианта
оптимального плана работы с затратами, равными 49 единицам: 3
; 4 ; 5 ; 0 и 4 ; 5 ; 0 ; 3.