Задачи дробно-линейного программирования

Если в задаче нелинейного программирования ограничения линейные, а целевая функция дробно-линейная, то ее называют задачей дробно-линейного программирования. Общий вид задачи дробно-линейного программирования: максимизировать (или минимизировать) функцию

(1)

при условиях

(2)

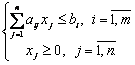
Симплексный метод

(3)

Во многих задачах с экономическим содержанием требуется, чтобы знаменатель целевой функции удовлетворял условию

.

При этом условии задачу дробно-линейного программирования можно решить симплексным методом.

Введем новые переменные. Обозначим

(4)

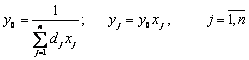
Тогда задача (1) - (3) примет вид

при ограничениях

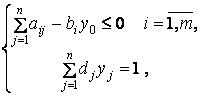
В результате получена задача линейного программирования. После ее решения симплексным методом, используя соотношения (4), можно найти оптимальное решение исходной задачи (1), (2).

Графический метод

Задачи дробно-линейного программирования с двумя переменными можно решать графически. Рассмотрим следующую задачу

(5)

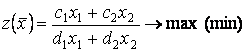
(6)

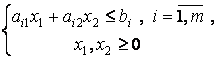
Будем считать, что .

Для решения этой задачи найдем многоугольник решений, определяемый ограничениями (6). Из выражения (5) найдем :

,

,

,

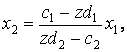
где 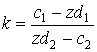, - прямая, проходящая через начало координат.

При фиксированном значении угловой коэффициент прямой тоже фиксирован. При изменении значений прямая будет поворачиваться вокруг начала координат.

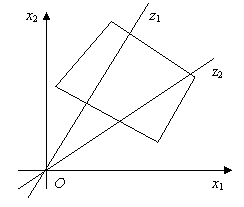Установим, как будет вести себя угловой коэффициент при монотонном возрастании . Найдем производную от по .

Знаменатель производной всегда положителен, а числитель от не зависит. Следовательно, производная имеет постоянный знак и при увеличении угловой коэффициент будет только возрастать или только убывать, при этом прямая будет поворачиваться вокруг точки О. Если угловой коэффициент прямой положителен, то прямая вращается против движения часовой стрелки, при отрицательном значении - по часовой стрелке. Установив направление вращения, находим вершину или вершины многогранника, в которых функция принимает экстремальное значение, либо делаем вывод о неограниченности функции. При этом возможны следующие случаи.

1. Многогранник решений ограничен, максимум и минимум достигаются в его угловых точках.

2. Многогранник решений не ограничен, однако существуют угловые точки, в которых целевая функция принимает максимальное и минимальное значения.

3. Многогранник решений не ограничен, один из экстремумов имеется. Например, минимум достигается в одной из вершин многогранника решений, т.е. имеет место так называемый асимптотический максимум.

4. Многогранник решений не ограничен. Максимум и минимум являются асимптотическими.

Алгоритм графического метода

1. Построить многогранник решений.

2. Определить угловой коэффициент и установить направление поворота линий уровня целевой функции.

3. Найти точку экстремума целевой функции или установить неразрешимость задачи.