Градиентный метод

Пример 1. Определить градиентным методом максимум функции ,

начиная итерационный процесс с точки .

Решение.

Определим градиент функции начальной точке .

.

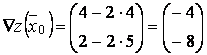Выбираем новую точку .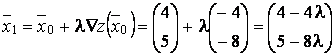

Найдем градиентфункции в новой точке:

.

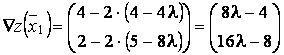Решаем уравнение

,

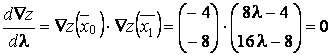откуда имеем

.

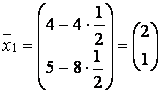и .

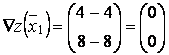Получен нулевой градиент, следовательно, точка является стационарной. Так как целевая функция является выпуклой (как сумма выпуклых функций и ), то в найденной точке достигается .

Ответ.

Пример 2. Минимизировать функцию при ограничениях

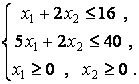
Решение. Систему ограничений запишем в виде

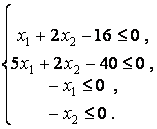
Определим градиентцелевой функции

.

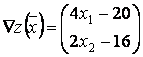Определим стационарную точку

.

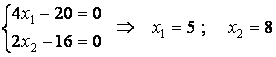Данная точка не является допустимой, так как не удовлетворяет системе ограничений. Следовательно, внутри области допустимых решений экстремума целевой функции нет, глобальный экстремум может достигаться только на границах или в вершинах области решений.

Рассмотрим граничную линию . Составим для нее систему

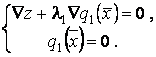где .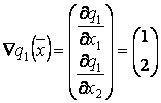

Имеем

или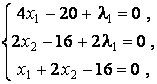

откуда получаем . Так как точка удовлетворяет системе ограничений и , то данная точка является стационарной.

Рассматриваем следующую граничную линию:

.

Для нее 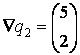и система имеет вид

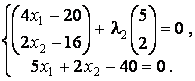или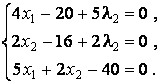

Решение этой системы: . Однако точка не удовлетворяет первому ограничению, следовательно, не является допустимой. Следующая граничная линия

,.

Имеем систему

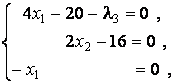
откуда . Так как , стационарных точек на грани нет.

Аналогично,

,.

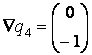Имеем систему

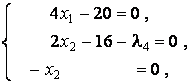
откуда . Так как , стационарных точек на грани нет.

Решая систему уравнений граничных линий, находим угловые точки области допустимых решений: . Находим значения в этих точках и ранее найденной точке

,

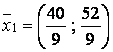Следовательно, при 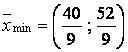.