ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Среди множества задач оптимизации особую роль в силу своей практической значимости играют задачи линейного программирования.

Пусть дана функция n переменных . Необходимо найти наибольшее или наименьшее значение этой функции при условии, что аргумент :

(1)

Поставленная таким образом задача оптимизации называется задачей математического программирования. Множество Х называется множеством допустимых решений, а функция 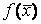- целевой функцией или функцией цели. Допустимое решение 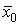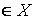, при котором функция принимает наибольшее (или наименьшее) значение, называется оптимальным решением задачи.

Если целевая функция является линейной, а множество Х задается с помощью системы линейных уравнений и неравенств, то задача (1) называется задачей линейного программирования (ЗЛП). Таким образом, общая постановка задачи линейного программирования такова: найти экстремум функции

при ограничениях:

.

В краткой записи задача линейного программирования имеет вид:

, .

Говорят, что задача линейного программирования представлена в канонической форме, если ее ограничения заданы в виде уравнений

.

Если в задаче линейного программирования ограничения заданы в виде неравенств

,

то говорят, что задача представлена в симметричной форме записи.

Переход от симметричной формы задачи к канонической осуществляется путем введения в каждое неравенство системы ограничений балансовой переменной, в результате чего ограничения принимают вид уравнений. В целевую функцию балансовые переменные вводятся с нулевыми коэффициентами.

Для осуществления перехода от канонической формы к симметричной форме задачи систему ограничений разрешают относительно произвольного базиса и, отбросив в уравнениях базисные переменные, сводят систему ограничений к системе неравенств. Целевую функцию выражают через свободные переменные.