МЕЖОТРАСЛЕВОЙ БАЛАНС

Модель Леонтьева

Межотраслевой баланс представляет собой таблицу, характеризующую взаимосвязи между объектами экономической системы. Предполагается, что экономическая система состоит из n отраслей, каждая из которых производит некоторый однородный продукт, отличный от продуктов других отраслей. Для производства своего продукта отрасль нуждается в продукции других отраслей (в качестве сырья, ресурсов, полуфабрикатов и т.д.), поэтому каждая отрасль представлена в таблице дважды: в качестве производителя и в качестве потребителя продукции других отраслей.

Введем следующие обозначения. Пусть x_ij - затраты продукта i-й отрасли на производственные нужды j-й отрасли, x_i – валовой продукт i-й отрасли, y_i – конечный продукт (конечное потребление) i-й отрасли, v_j – условно-чистая продукция j-й отрасли за некоторый промежуток времени (год, квартал и т.д.). Перечисленные показатели приводятся в стоимостном выражении.

Общий вид межотраслевого баланса представим в виде таблицы.

Потребление Производство	P1	P2	…	Pn	Конечное потребление Yi	Валовой продукт Xi
P1	x11	x12	…	x1n	y1	x1
P2	x21	x22	…	x2n	y2	x2
…	…	…	…	…	…	…
Pn	xn1	xn2	…	xnn	yn	xn
Условно-чистая продукция Vj	v1	v2	…	vn
Валовой продукт Xj	x1	x2	…	xn

Таблица состоит из четырех квадрантов, разделенных на рисунке двойными линиями. Верхний левый квадрант характеризует межотраслевые потоки продукции. Строки этого раздела показывают распределение продукции каждой отрасли на нужды других отраслей. Столбцы отражают структуру производственного потребления отраслей.

Правый верхний квадрант содержит два столбца: столбец Y_i содержит объемы конечного продукта отраслей (в его состав входят: продукция отрасли, предназначенная к потреблению в непроизводственной сфере (личное потребление), обеспечение общественных потребностей, возмещение выбытия основных фондов, экспортные поставки, накопление). Столбец X_i содержит величины общего объема продукции отраслей, т.е. валовой продукт.

Нижний левый квадрант, кроме строки X_j, содержит строку V_j величин условно-чистой продукции отраслей, включающих амортизационные отчисления, заработную плату и прибыль.

Важным свойством таблицы является то, что для любой строки с номером справедливо соотношение баланса между производством и потреблением:

x_i=+y_i (1)

означающее, что валовой продукт отрасли расходуется полностью — на производственное (промежуточное) и непроизводственное (конечное) потребление.

Аналогично, для любого столбца с номером справедливо равенство

x_j=+v_j (2)

Равенство (2) представляет стоимостную структуру продукта каждой отрасли. Оно показывает, что стоимость валового продукта отрасли складывается из затрат других отраслей на его производство и стоимости условно-чистой продукции, не производящейся внутри производственной системы.

Отметим и еще одно важное соотношение межотраслевого баланса: суммарный конечный продукт равен суммарной условно-чистой продукции:

(3)

Построим математическую модель межотраслевого баланса. Предположим, что для выпуска некоторого объема продукции x_ij необходимо затратить валовую продукцию j-й отрасли в количестве a_ijx_j, где a_ij – постоянный коэффициент, обусловленный существующими технологиями производства и определяемый, например, по данным отчетного баланса. Соотношение

x_ij=a_ijx_j (4)

выражает условие линейной зависимости объема производства от издержек или линейности существующей технологии. Коэффициенты

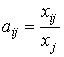, (5)

где называют коэффициентами прямых материальных затрат или технологическими коэффициентами. Каждый коэффициент a_ij есть стоимость продукции i-й отрасли, вложенной в производство единицы продукции j-й отрасли в стоимостном выражении. Матрицу , называют матрицей прямых материальных затрат.

Технологические коэффициенты имеют следующие свойства:

;

; .

Используя соотношения (1) и (4), составим линейную балансовую модель:

(6)

или в матричной форме:

, (7)

где А – матрица коэффициентов прямых материальных затрат, Е – единичная матрица порядка n, - вектор конечного потребления, - вектор валового выпуска. Полученную систему (7) называют моделью Леонтьева. В системе содержится 2n неизвестных в n линейных уравнениях. Если задать n из них, то система будет определенной. Поэтому задачи, решаемые с помощью балансовой модели, можно разделить на три группы:

1) По заданному вектору конечного потребления найти вектор валового выпуска . Решение матричного уравнения (7) относительно имеет вид:

2) По заданному вектору валового выпуска найти вектор конечного потребления . Решив матричное уравнение (7), относительно , получим:

3) Смешанная задача: по некоторым заданным x_i и y_j найти соответствующие x_j и y_i.

Рассмотрим более подробно первую задачу. Она содержит основной вопрос межотраслевого анализа: каким должно быть валовое производство каждой отрасли, чтобы экономическая система в целом произвела заданное количество конечного продукта. Разрешимость уравнения (7) в положительных числах зависит от свойства матрицы А, называемого продуктивностью матрицы.

Матрица А называется продуктивной, если существует вектор такой, что . Смысл последнего неравенства состоит в том, что затраты на выпуск продукта должны быть меньше стоимости самого продукта. Достаточным условием продуктивности матрицы является выполнение условий:

; .

Если матрица А - продуктивная, то для любого существует неотрицательное решение уравнения (7).

Для того, чтобы матрица А была продуктивной, необходимо и достаточно, чтобы существовала неотрицательная матрица

Матрицу В называют матрицей полных материальных затрат или обратной матрицей Леонтьева. Таким образом, решение уравнения (7) относительно можно найти по формуле:

или в координатной форме

, .