Задача на безусловный экстремум

Пример 1. Исследовать на экстремум функцию

.

Решение. Найдем стационарные точки функции из условий

, .

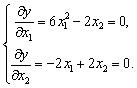
Данная система имеет два решения

или

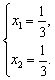
Найдены две стационарные точки: А(0;0) и В. Проверим, являются ли они точками экстремума. Составим матрицу Гессе и вычислим ее значение в точке А.

Вычислим главные диагональные миноры матрицы

М₁ = 0;

М₂ =.

Следовательно, точка А не является точкой экстремума функции.

Составим матрицу Гессе в точке В:

Вычислим главные диагональные миноры матрицы

М₁ = 4 > 0;

М₂ =.

Следовательно, точка В является точкой минимума функции,

, .

Пример 2. Исследовать на экстремум функцию

.

Решение. Найдем стационарную точку из условий

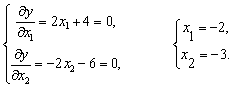
Итак, .

Исследуем статус этой точки, т.е. проверим, является ли она точкой экстремума. Для этого вычислим матрицу Гессе:

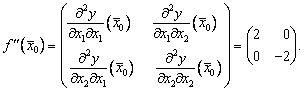
Вычислим главные диагональные миноры матрицы Гессе.

М₁ = 2

М₂ =

Минор второго порядка отрицателен, значит, в точке экстремума нет.