Гипербола

Определение 1. Геометрическое место точек, модуль разности расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, называется гиперболой.

Выведем уравнение гиперболы. Обозначим постоянную величину из определения гиперболы 2а, расстояние между фокусами - 2с. Очевидно, с > а. Введем систему координат: ось OX проходит через фокусы, ось OY через середину отрезка, соединяющего фокусы. В данной системе фокусы имеют координаты F₁(-c,0) и F₂(c,0). Возьмем произвольную точку M (x, y) на гиперболе и составим уравнение, связывающее ее координаты x и y (рис. 1).

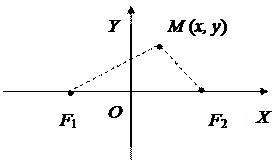
Рис. 1

По определению гиперболы |MF₁ - MF₂| = 2a, отсюда:

.

Освободимся в последнем равенстве от радикалов и модуля двойным возведением в квадрат обеих частей равенства. В результате получим:

.

Обозначим . Тогда последнее равенство примет вид:

Разделив обе части на a²b², получим:

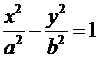— каноническое уравнение гиперболы.

Исследуем форму гиперболы.

1. Найдем точки пересечения с осями.

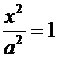OX: y = 0, , , A (a; 0), B (–a; 0).

OY: x = 0, , .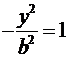

Определение 2. Точки A и B называются вершинами гиперболы.

2. Из вида уравнения следует, что линия симметрична относительно осей OX, OY и начала координат.

3. 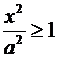Þ Þ .

Следовательно, кривая расположена вне прямоугольника со сторонами 2а и 2b.

Построим данную кривую (рис. 2).

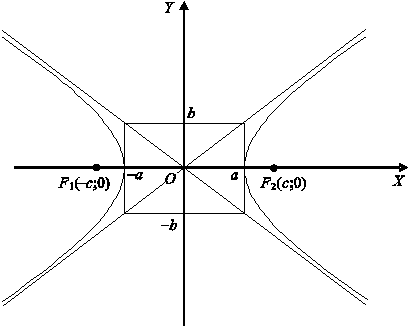
Рис.2

Определение 3. Параметр a называется действительной полуосью гиперболы, а параметр b называется мнимой полуосью.

Определение 4. Прямые 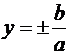называются асимптотами гиперболы.

При возрастании х гипербола неограниченно приближается к асимптотам.

Определение 5. Отношение фокусного расстояния гиперболы к ее действительной оси называется эксцентриситетом.

.

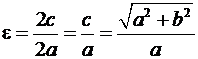Определение 6. Кривые эллипс, гипербола, окружность называются кривыми второго порядка с эксцентриситетом, причем для окружности , для эллипса и для гиперболы . При гипербола вырождается в две параллельные прямые.