Угол между двумя прямыми.

Условие параллельности

и перпендикулярности прямых

Определение 1. Углом между двумя прямыми I и II называется угол, отсчитываемый в положительном направлении от прямой I к прямой 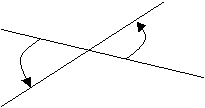II.

II

I

Пусть даны две прямые, заданные уравнениями с угловыми коэффициентами

y = k₁ · x + b₁, y = k₂ · x + b₂.

Найдем угол между первой и второй прямыми. Обозначим углы наклона прямых j₁ и j₂. Тогда

k₁ = tgj₁ , k₂ = tgj₂.

Проведем через точку пересечения прямую, параллельную оси OX.

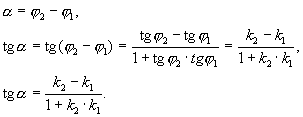
- формула для вычисления угла между двумя прямыми.

1. Предположим, что прямые параллельны:

a = 0 Þ tg a = 0 Þ

k₁ = k₂ - условие параллельности прямых.

2. Предположим, что прямые перпендикулярны:

a = 90⁰ Þ tg a не существует Þ ctg a = 0 Þ

Þ k₁ · k₂ = -1 - условие перпендикулярности прямых.