Уравнение прямой, проходящей

через данную точку в данном направлении

Предположим, что прямая проходит через точку M₁ (x₁,y₁) и образует с осью OX угол j. Составим уравнение этой прямой.

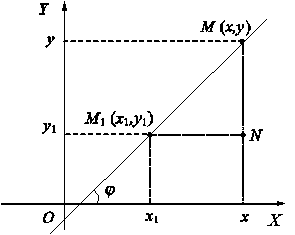
Будем искать уравнение прямой в виде уравнения с угловым коэффициентом: y = k · x + b. Угловой коэффициент прямой можно найти, зная угол наклона k = tg j. Возьмем произвольную точку M (x, y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Так как точки М и M₁ лежат на прямой, то их координаты удовлетворяют уравнению прямой:

y = k · x + b,

y₁ = k · x₁ + b.

Вычитая эти равенства, получим:

y - y₁ = k · (x - x₁) - уравнение прямой, проходящей через данную точку в данном направлении.