Уравнение прямой с угловым коэффициентом

Предположим, что прямая расположена под углом j к оси ОХ и отсекает от оси ОУ отрезок в b единиц. Составим уравнение этой прямой.

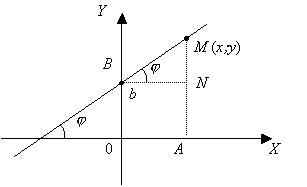
Возьмем произвольную точку M (x, y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Из рисунка видно: AM = AN + NM, где AM = y, AN = b. Из треугольника BMN: MN = BN · tg j. Обозначим tg j = k и назовем его угловым коэффициентом прямой. MN = k · x.

Подставляя в равенство

AM = AN + NM

выражения отрезков

AM = y, AN = b, MN = k · x;

получим

y = k · x + b - уравнение прямой с угловым коэффициентом.