Общее уравнение прямой

Теорема 1. Всякое невырожденное уравнение первой степени с двумя переменными определяет на плоскости некоторую прямую, и наоборот.

Аx+Вy+С=0 - общее уравнение прямой,

- условие невырожденности.

Рассмотрим различные случаи расположения прямой на плоскости в зависимости от коэффициентов общего уравнения.

1) С = 0, Ax + By = 0 - прямая проходит через начало координат;

А = 0, By + C = 0 - прямая проходит параллельно оси ОХ;

В = 0, Ax + C = 0 - прямая проходит параллельно оси ОУ;

2) A = C = 0, By = 0 - прямая совпадает с осью ОХ;

B = C = 0, Ax = 0 - прямая совпадает с осью ОУ.

Расстояние от точки M₀ (x₀,y₀) до прямой, заданной общим уравнением Ax + By + C = 0, находится по формуле

.
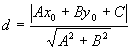