Декартова прямоугольная система координат

 

Определение 1. Осью называется прямая, на которой:

1)  выбрана начальная точка ("начало" - точка О);

2)  указано (стрелкой) положительное направление отсчета;

3)  выбран масштаб.

Определение 2. Декартовой прямоугольной системой координат на плоскости (в пространстве) называют две (три) взаимно перпендикулярные оси с общим началом. Первая ось OX называется осью абсцисс, вторая ось OY - осью ординат (третья ось OZ - осью аппликат).

Каждой точке плоскости (пространства) ставится в соответствие упорядоченная пара (тройка) действительных чисел - координат данной точки.

Определение 3. Уравнением линии на плоскости называется уравнение с двумя переменными, такое, что только координаты любой точки, лежащей на этой линии, удовлетворяют данному уравнению.

Расстояние между двумя точками на плоскости

Даны две точки на плоскости с координатами A (x1, y1) и B (x2, y2).

9

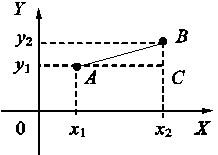
Из треугольника ABC:

.

Деление отрезка в данном отношении

Пусть даны две точки M1 (x1, y1) и M2 (x2, y2). Найдем на отрезке M1M2 точку N, которая делила бы данный отрезок в отношении : .

9

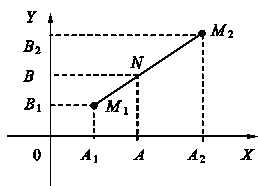
По теореме о пропорциональности отрезков прямых, пересеченных рядом параллельных прямых, получим

,

,

              

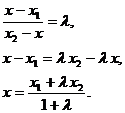
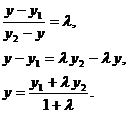
Координаты точки, делящей отрезок в данном отношении, находятся по этим формулам.

Если l = 1 , то деление отрезка производится пополам:

 ,  - формулы для нахождения координат середины отрезка.