Уравнение плоскости, проходящей

через данную точку перпендикулярно

данному вектору

Пусть плоскость проходит через точку M₀ (x₀, y₀, z₀) и перпендикулярна вектору (M, N, L). Вектор (M, N, L) называется вектором нормали к плоскости.

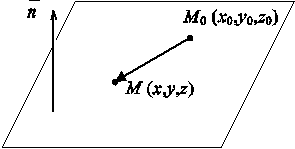
Возьмем произвольную точку M(x, y, z), лежащую в этой плоскости, и найдем связь между координатами x, y, z в виде уравнения. Рассмотрим вектор .

Векторы и ортогональны. Следовательно, · = 0.

M(x - x₀) + N(y - y₀) + L(z - z₀) = 0

- уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору. Если раскрыть скобки в этом уравнении, то его можно привести Mx + Ny + Lz + К = 0,

где К= - Mx₀ - Ny₀ - Lz₀. Следовательно, если плоскость задана общим уравнением Ax + By + Cz + D = 0, то вектор (A,B,C) является вектором нормали к плоскости.