Уравнение плоскости в пространстве

Теорема. Всякое невырожденное уравнение первой степени с тремя переменными описывает некоторую плоскость в пространстве, и наоборот: всякая плоскость может быть описана таким уравнением.

Ax + By + Cz + D = 0 - общее уравнение плоскости,

A² + B² + C² ¹ 0 - условие невырожденности.

Рассмотрим различные случаи расположения плоскости в пространстве в зависимости от коэффициентов общего уравнения.

1. D = 0, Ax + By + Cz = 0 - проходит через начало координат;

A = 0, By + Cz + D = 0 - параллельна оси ОХ;

B = 0, Ax + Cz + D = 0 - параллельна оси OY;

C = 0, Ax + By + D = 0 - параллельна оси OZ;

2. A = D = 0, By + Cz = 0 - содержит OX;

B = D = 0, Ax + Cz = 0 - содержит OY;

C = D = 0, Ax + By = 0 - содержит OZ;

A = B = 0, Cz + D = 0 - параллельна плоскости XOY;

A = C = 0, By + D = 0 - параллельна плоскости XOZ;

B = C = 0, Ax + D = 0 - параллельна плоскости YOZ;

3. A = B = D = 0, Cz = 0 - совпадает с плоскостью XOY;

A = C = D = 0, By = 0 - совпадает с плоскостью XOZ;

B = C = D = 0, Ax = 0 - совпадает с плоскостью YOZ.

Расстояние от точки M₀ (x₀, y₀, z₀) до плоскости, заданной общим уравнением Ax + By + Cz + D = 0, вычисляется по формуле

.
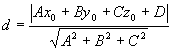