Поворот системы координат

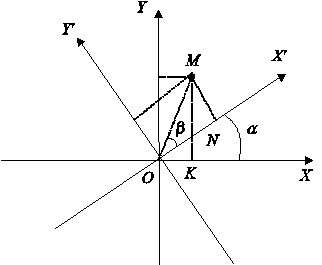
Предположим, что прямоугольную систему координат повернули на угол a в положительном направлении и получили новую систему координат .

Эти соотношения описывают преобразование координат при повороте, они выражают старые координаты через новые. Из этих соотношений можно выразить новые координаты. Выражение новых координат через старые:

Пример 1. Кривая второго порядка задана уравнением

.

Приведем его к каноническому виду. Сделаем преобразование: поворот на угол a = 45⁰.

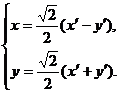
Найдем уравнение этой линии в новой системе координат :

Получили каноническое уравнение эллипса с параметрами a = 4 и b = 2.

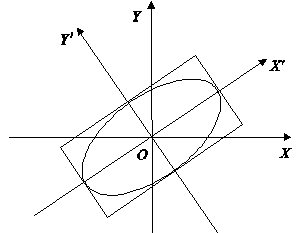
Пример 2. Построим график дробно-линейной функции

,

где с¹0, bc-ad¹0. Преобразуем выражение для функции:

.

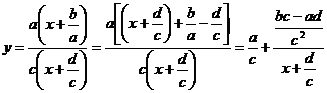Обозначим и введем новые координаты

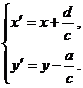
Эти уравнения описывают параллельный перенос системы координат. Центр координат перейдет в точку . В новой системе координат уравнение имеет вид: . Сделаем преобразование: поворот на угол a = 45⁰.

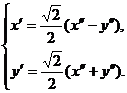
Найдем уравнение этой линии в новой системе координат :

.

Мы получили каноническое уравнение равносторонней гиперболы с асимптотами , (рис. 2.20).

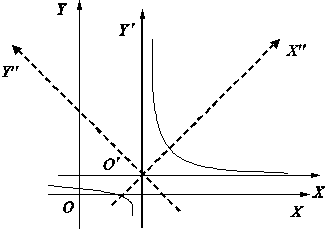
Таким образом, графиком дробно-рациональной функции является равносторонняя гипербола.