Параллельный перенос системы координат
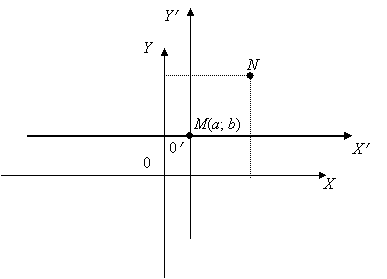
Предположим, что система
координат XOY
перенесена параллельно себе так, что начало координат сместилось в точку M(a;b). Найдем связь между координатами
любой точки в старой и новой системе координат. Возьмем произвольную точку N. В плоскости XOY она имеет координаты N(x; y), в плоскости ![]() она имеет координаты
она имеет координаты ![]() .
.
![]()
![]()
- преобразование координат при параллельном переносе; выражение старых координат через новые и новых через старые.
Пример 1. Рассмотрим уравнение:
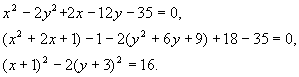
Совершим параллельный перенос по формулам
![]()
При этом начало координат перейдет
в точку ![]() . В новой системе координат уравнение примет вид
. В новой системе координат уравнение примет вид
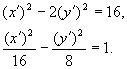
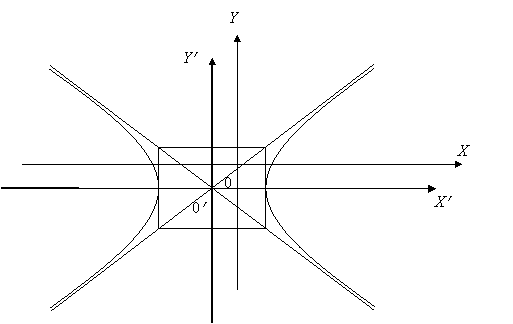
В новой системе координат ![]() получено каноническое
уравнение гиперболы с параметрами a = 4, b =
получено каноническое
уравнение гиперболы с параметрами a = 4, b = ![]() .
.
Построим старые и новые оси, а также саму кривую.
Пример 2. Рассмотрим квадратный трехчлен
![]() .
.
Построим его график. Для этого преобразуем уравнение
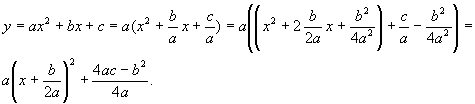
Введем новые координаты по формулам
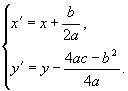
Тогда в новой системе координат ![]() , полученной параллельным переносом осей координат с новым
центром в точке
, полученной параллельным переносом осей координат с новым
центром в точке ![]() , уравнение примет вид
, уравнение примет вид
![]() ,
,
где р=1/2a.
Таким
образом, графиком квадратного трехчлена является парабола
с вершиной в точке ![]() с осью симметрии
с осью симметрии ![]() , параллельной оси OY.
, параллельной оси OY.