Парабола

Определение 1. Геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой, именуется параболой.

Выведем уравнение параболы. Обозначим расстояние от фокуса до директрисы р. Введем систему координат: ось OX проходит через фокус перпендикулярно директрисе, ось OY через середину отрезка перпендикуляра, опущенного из фокуса на директрису. В данной системе фокус имеют координаты . Возьмем произвольную точку M (x, y) на параболе (рис. 1) и составим уравнение, связывающее ее координаты x и y.

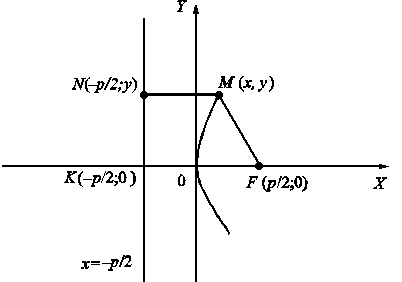
Рис. 1

По определению параболы MN = MF, отсюда:

.

Освободимся в последнем равенстве от радикалов возведением в квадрат обеих частей равенства. В результате получим:

— каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси OX.

Исследуем форму параболы.

1. Найдем точки пересечения с осями.

OX, OY: y = 0, х = 0, О (0; 0).

Определение 2. Точка О называется вершиной параболы.

2. Из вида уравнения следует, что линия симметрична относительно оси OX.

3. . Следовательно, кривая расположена правее оси OY.

Построим данную кривую (см. рис. 2.14).

Если парабола симметрична относительно OY и имеет вершину в начале координат, то ее каноническое уравнение имеет вид (рис. 2).

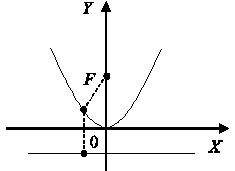
Рис. 2