Применение линейной алгебры в экономике

Производственные показатели

Предприятие выпускает ежесуточно четыре вида изделий, основные производственно-экономические показатели которых приведены в следующей таблице:

Вид изделий	Количество изделий	Расход сырья, кг/изд.	Норма времени изготовления, ч/изд.	Цена изделия, ден. ед./изд.
1 2 3 4	20 50 30 40	5 2 7 4	10 5 15 8	30 15 45 20

Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.

По приведенным данным составим четыре вектора, характеризующие весь производственный цикл:

= (20, 50, 30, 40) - вектор ассортимента;

= (5, 2, 7, 4) - вектор расхода сырья;

= (10, 5, 15, 8) - вектор затрат рабочего времени;

= (30, 15, 45, 20) - ценовой вектор.

Тогда искомые величины будут представлять собой соответствующие скалярные произведения вектора ассортимента на три других вектора:

S= = 100 + 100 + 210 + 160 = 570 кг,

Т = = 1220 ч, P= = 3500 ден. ед.

Расход сырья

Предприятие выпускает четыре вида изделий с использованием четырех видов сырья. Нормы расхода сырья даны как элементы матрицы А:

Вид сырья

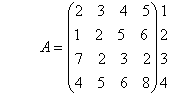Вид изделия.

Требуется найти затраты сырья каждого вида при заданном плане выпуска каждого вида изделия: соответственно, 60, 50, 35 и 40 ед.

Составим вектор-план выпуска продукции:

=(60, 50, 35, 40).

Тогда решение задачи дается вектором затрат, координаты которого и являются величинами затрат сырья по каждому его виду: этот вектор затрат вычисляется как произведение вектора на матрицу А:

.

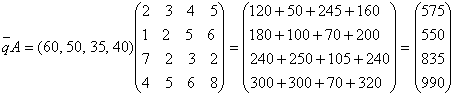Конечный продукт отрасли

Отрасль состоит из п предприятий, выпускающих по одному виду продукции каждое: обозначим объем продукции i-го предприятия через х_i. Каждое из предприятий отрасли для обеспечения своего производства потребляет часть продукции, выпускаемой им самим и другими предприятиями. Пусть а_ij - доля продукции i-го предприятия, потребляемая j-м предприятием для обеспечения выпуска своей продукции объема х_j. Найдем величину у_i - количество продукции i-го предприятия, предназначенной для реализации вне данной отрасли (объем конечного продукта). Эта величина легко может быть подсчитана по формуле

Введем в рассмотрение квадратную матрицу порядка п, описывающую внутреннее потребление отрасли

Тогда вектор конечного продукта является решением матричного уравнения

с использованием единичной матрицы Е получаем

Пример. Пусть вектор выпуска продукции отрасли и матрица внутреннего потребления имеют, соответственно, вид

.

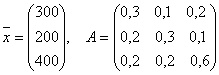Получим вектор объемов конечного продукта, предназначенного для реализации вне отрасли, состоящей из трех предприятий:

.

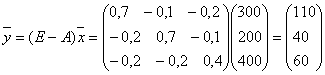Прогноз выпуска продукции

Пусть - матрица затрат сырья т видов при выпуске продукции п видов. Тогда при известных объемах запаса каждого вида сырья, которые образуют соответствующий вектор

вектор-план выпуска продукции определяется из решения системы т уравнений с п неизвестными:

где индекс "т" означает транспонирование вектора-строки в вектор-столбец.

Пример. Предприятие выпускает три вида продукции, используя сырье трех видов. Необходимые характеристики производства представлены следующими данными:

Вид сырья	Расход сырья по видам продукции, вес. ед./изд.			Запас сырья, вес. ед.
	1	2	3
1 2 3	6 4 5	4 3 2	5 1 3	2400 1450 1550

Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья.

Задачи такого рода типичны при прогнозах и оценках функционирования предприятий, экспертных оценках проектов освоения месторождений полезных ископаемых, а также в планировании микроэкономики предприятий.

Обозначим неизвестные объемы выпуска продукции через х₁, х₂ и х₃. Тогда при условии полного расхода запасов каждого вида сырья можно записать балансовые соотношения, которые образуют систему трех уравнений с тремя неизвестными:

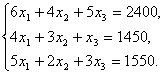
Решая эту систему уравнений любым способом, находим, что при заданных запасах сырья объемы выпуска продукции составят по каждому виду соответственно (в условных единицах):

.

Линейная модель многоотраслевой экономики

Для простоты будем полагать, что производственная сфера хозяйства представляет собой п отраслей, каждая из которых производит свой однородный продукт. Для обеспечения производства каждая отрасль нуждается в продукции других отраслей (производственное потребление). Обычно процесс производства рассматривается за некоторый период; в ряде случаев такой единицей служит год.

Введем следующие обозначения:

- общий объем продукции i-й отрасли;

- объем продукции i-й отрасли, потребляемый j-й отраслью при производстве объема продукции ;

- объем продукции i-й отрасли, предназначенный для реализации (потребления) в непроизводственной сфере, или так называемый продукт конечного потребления.

Балансовый принцип связи различных отраслей промышленности состоит в том, что валовой выпуск i-й отрасли должен быть равен сумме объемов потребления в производственной и непроизводственной сферах. В самой простой форме (гипотеза линейности, или простого сложения) балансовые соотношения имеют вид

Эти уравнения называются соотношениями баланса. Поскольку продукция разных отраслей имеет разные измерения, в дальнейшем будем иметь в виду стоимостный баланс.

В. Леонтьевым на основании анализа экономики США в период перед второй мировой войной был установлен важный факт: в течение длительного времени величины меняются очень незначительно и могут рассматриваться как постоянные числа. Это явление становится понятным в свете того, что технология производства остается на одном и том же уровне довольно длительное время, и, следовательно, объем потребления j-й отраслью продукции i-й отрасли при производстве своей продукции объема есть технологическая константа.

В силу указанного факта можно сделать следующее допущение: для производства продукции j-й отрасли объема нужно использовать продукцию i-й отрасли объема , где - постоянное число. При таком допущении технология производства принимается линейной, а само это допущение называется гипотезой линейности. При этом числа называются коэффициентами прямых затрат. Согласно гипотезе линейности

.

Соотношения баланса можно переписать в виде системы уравнений

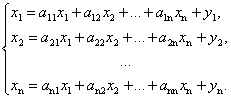
Введем в рассмотрение векторы-столбцы объемов произведенной продукции (вектор валового выпуска), объемов продукции конечного потребления (вектор конечного потребления) и матрицу коэффициентов прямых затрат:

.

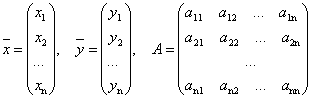Тогда система уравнений в матричной форме имеет вид

Обычно это соотношение называют уравнением линейного межотраслевого баланса. Вместе с описанием матричного представления это уравнение носит название модели Леонтьева.

Уравнение межотраслевого баланса можно использовать в двух целях. В первом (наиболее простом) случае, когда известен вектор валового выпуска , требуется рассчитать вектор конечного потребления . Во втором случае уравнение межотраслевого баланса используется для целей планирования со следующей формулировкой задачи: для периода Т (например, год) известен вектор конечного потребления , требуется определить вектор валового выпуска.

Линейная модель торговли

Процесс взаимных закупок товаров анализируется с использованием понятий собственного числа и собственного вектора матрицы. Будем полагать, что бюджеты n стран, которые мы обозначим, соответственно, х₁, х₂, …, х_n, расходуются на покупку товаров. Рассмотрим линейную модель обмена, или модель международной торговли.

Пусть а_ij - доля бюджета х_j, которую j-я страна тратит на закупку товаров у i-й страны. Введем матрицу коэффициентов а_ij:

.

Тогда, если весь бюджет расходуется только на закупки внутри страны и вне ее (это можно трактовать как торговый бюджет), справедливо равенство

Матрица А с данным свойством, в силу которого сумма элементов ее любого столбца равна единице, называется структурной матрицей торговли. Для i-й страны общая выручка от внутренней и внешней торговли выражается формулой

.

Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е. , или

.

Докажем, что в условиях не может быть знака неравенства. Действительно, сложим все эти неравенства при i от 1 до п. Группируя слагаемые с величинами бюджетов , получаем

.

Нетрудно заметить, что в скобках стоят суммы элементов матрицы А по ее столбцам, которые равны единице по условию. Стало быть, мы получили неравенство

,

откуда следует, что возможен только знак равенства.

Таким образом, условия принимают вид равенств:

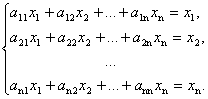
Введем вектор бюджетов , каждая компонента которого характеризует бюджет соответствующей страны. Тогда систему уравнений можно записать в матричной форме:

Это уравнение означает, что собственный вектор структурной матрицы А, отвечающий ее собственному значению l=1, состоит из бюджетов стран бездефицитной международной торговли. Перепишем уравнение в виде, позволяющем определить :

Пример. Структурная матрица торговли четырех стран имеет вид

.

Найти бюджеты этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов задана:

.

Решение. Необходимо найти собственный вектор , отвечающий собственному значению l=1 заданной структурной матрицы А, т.е. решить уравнение, которое в нашем случае имеет вид

.

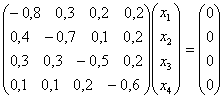Поскольку ранг этой системы равен трем, то одна из неизвестных является свободной переменной, остальные выражаются через нее. Решая систему методом Гаусса, находим компоненты собственного вектора :

.

Подставив найденные значения в заданную сумму бюджетов, определим величину с:

с=1210.

Откуда окончательно получаем искомые величины бюджетов стран при бездефицитной торговле:

.