Интерполяционная формула Лагранжа.

Задача. На отрезке , заданы значения неизвестной функции в различных точках:

Требуется найти многочлен степени не выше , приближенно выражающий функцию . В качестве такого многочлена можно взять многочлен, значения которого в точках совпадает с . Данная задача является задачей интерполирования функции.

В качестве искомого многочлена возьмем многочлен -степени вида.

.

Определим коэффициент , так, чтобы , .

Положим ,

,

.

Положим ,

,

.

Аналогично:

,

...

.

Таким образом многочлен имеет вид:

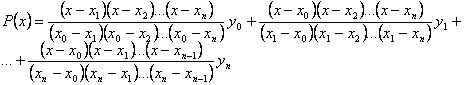
- интерполяционная формула Лагранжа.

Пример. Дана таблица значений некоторой функции

	1	2	-4
	3	-5	4

Требуется представить функцию -многочленом второй степени.

.

.